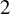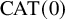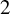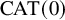1 Introduction
A triangle complex X is a 2-dimensional simplicial complex, possibly not locally compact, with a following piecewise smooth Riemannian metric. Namely, we have a family of smooth Riemannian metrics
![]() $\sigma _T, \sigma _e$
on the triangles and edges, such that the restriction of
$\sigma _T, \sigma _e$
on the triangles and edges, such that the restriction of
![]() $\sigma _T$
to e is
$\sigma _T$
to e is
![]() $\sigma _e$
for each
$\sigma _e$
for each
![]() $e\subset T$
. The Riemannian metrics
$e\subset T$
. The Riemannian metrics
![]() $\sigma _T, \sigma _e$
induce metrics (i.e. distance functions) on triangles and edges. We then equip X with the quotient pseudometric d (see [Reference Bridson and HaefligerBH99, Chapter I.5.19]). We assume that for each metric ball B, the simplices of X intersecting B have only finitely many isometry types (note that the only time we will apply it to B of radius nonzero is in the proof of Remark 2.5). Then
$\sigma _T, \sigma _e$
induce metrics (i.e. distance functions) on triangles and edges. We then equip X with the quotient pseudometric d (see [Reference Bridson and HaefligerBH99, Chapter I.5.19]). We assume that for each metric ball B, the simplices of X intersecting B have only finitely many isometry types (note that the only time we will apply it to B of radius nonzero is in the proof of Remark 2.5). Then
![]() $(X,d)$
is a complete length space, which can be deduced from [Reference Bridson and HaefligerBH99, Chapters I.5.20 and I.7.13] using a bilipschitz map from each B to a piecewise Euclidean complex. Note that we study triangle complexes, as opposed to piecewise Euclidean 2-dimensional simplicial complexes, for applications to groups such as
$(X,d)$
is a complete length space, which can be deduced from [Reference Bridson and HaefligerBH99, Chapters I.5.20 and I.7.13] using a bilipschitz map from each B to a piecewise Euclidean complex. Note that we study triangle complexes, as opposed to piecewise Euclidean 2-dimensional simplicial complexes, for applications to groups such as
![]() $\mathrm {Tame}(\mathbf k^3)$
(Corollary D). All group actions on X will be by simplicial isometries.
$\mathrm {Tame}(\mathbf k^3)$
(Corollary D). All group actions on X will be by simplicial isometries.
We say that a group acts on a cell complex X almost freely if there is a bound on the order of the cell stabilisers. Note that an almost free action on a triangle complex is proper in the sense of [Reference Bridson and HaefligerBH99, Chapter I.8.2]. Furthermore, any subgroup of a group acting properly and cocompactly acts almost freely. A group is virtually cyclic (respectively, virtually
![]() $\mathbb {Z}^2$
, virtually abelian, virtually solvable), if it has a finite index subgroup that is cyclic (respectively,
$\mathbb {Z}^2$
, virtually abelian, virtually solvable), if it has a finite index subgroup that is cyclic (respectively,
![]() $\mathbb {Z}^2$
, abelian, solvable).
$\mathbb {Z}^2$
, abelian, solvable).
Theorem A. Let G be a finitely generated group acting almost freely on a
![]() $\mathrm {CAT}(0)$
triangle complex X. Then G is virtually cyclic, or virtually
$\mathrm {CAT}(0)$
triangle complex X. Then G is virtually cyclic, or virtually
![]() $\mathbb {Z}^2$
, or it contains a nonabelian free group.
$\mathbb {Z}^2$
, or it contains a nonabelian free group.
By [Reference Bridson and HaefligerBH99, Chapters II.7.5 and 7.7(2)] and Remarks 2.4 and 2.5, if G acts almost freely on a
![]() $\mathrm {CAT(0)}$
triangle complex with finitely many isometry types of simplices, then every sequence
$\mathrm {CAT(0)}$
triangle complex with finitely many isometry types of simplices, then every sequence
![]() $G_1<G_2<\cdots $
of virtually abelian subgroups of G stabilises. Consequently:
$G_1<G_2<\cdots $
of virtually abelian subgroups of G stabilises. Consequently:
Corollary B. If X has finitely many isometry types of simplices, then Theorem A holds also for G infinitely generated.
As explained in [Reference Osajda and PrzytyckiOP21, page 3], one cannot omit in Theorem A the assumption on almost freeness.
Here are some examples of applications of Theorem A to particular groups. The first result, which is a consequence of Corollary B, was studied independently by Paul Tee. We are assuming that G below acts freely instead of almost freely, since A is torsion free [Reference Charney and DavisCD95, Theorem B].
Corollary C. Let G be a subgroup of a
![]() $2$
-dimensional Artin group A acting freely on the modified Deligne complex of A (see [Reference Charney and DavisCD95]). Then G is cyclic,
$2$
-dimensional Artin group A acting freely on the modified Deligne complex of A (see [Reference Charney and DavisCD95]). Then G is cyclic,
![]() $\mathbb {Z}^2$
, the fundamental group of the Klein bottle, or it contains a nonabelian free group.
$\mathbb {Z}^2$
, the fundamental group of the Klein bottle, or it contains a nonabelian free group.
The second result concerns the tame automorphism group
![]() $\mathrm {Tame}(\mathbf k^3)$
, which is a subgroup of
$\mathrm {Tame}(\mathbf k^3)$
, which is a subgroup of
![]() $\mathrm {Aut}(\mathbf k^3)$
, where
$\mathrm {Aut}(\mathbf k^3)$
, where
![]() $\mathbf k$
is a field (see [Reference Lamy and PrzytyckiLP21]). In [Reference Lamy and PrzytyckiLP21, Sections 2 and 5], we introduced a cell complex
$\mathbf k$
is a field (see [Reference Lamy and PrzytyckiLP21]). In [Reference Lamy and PrzytyckiLP21, Sections 2 and 5], we introduced a cell complex
![]() $\textbf {X}$
with an action of
$\textbf {X}$
with an action of
![]() $\mathrm {Tame}(\mathbf k^3)$
. We proved that
$\mathrm {Tame}(\mathbf k^3)$
. We proved that
![]() $\textbf {X}$
is
$\textbf {X}$
is
![]() $\mathrm {CAT(0)}$
for
$\mathrm {CAT(0)}$
for
![]() $\mathbf k$
of characteristic
$\mathbf k$
of characteristic
![]() $0$
[Reference Lamy and PrzytyckiLP21, Theorem A]. Some cells of
$0$
[Reference Lamy and PrzytyckiLP21, Theorem A]. Some cells of
![]() $\textbf {X}$
are polygons instead of triangles, but we can easily transform
$\textbf {X}$
are polygons instead of triangles, but we can easily transform
![]() $\textbf {X}$
into a triangle complex by subdividing.
$\textbf {X}$
into a triangle complex by subdividing.
Corollary D. Let G be a finitely generated subgroup of
![]() $\mathrm {Tame}(\mathbf k^3)$
, with
$\mathrm {Tame}(\mathbf k^3)$
, with
![]() $\mathbf k$
of characteristic
$\mathbf k$
of characteristic
![]() $0$
. Suppose that G acts almost freely on the cell complex
$0$
. Suppose that G acts almost freely on the cell complex
![]() $\mathbf X$
. Then G is virtually cyclic, or virtually
$\mathbf X$
. Then G is virtually cyclic, or virtually
![]() $\mathbb {Z}^2$
, or it contains a nonabelian free group.
$\mathbb {Z}^2$
, or it contains a nonabelian free group.
An ingredient in the proof of Theorem A is the following characterisation of
![]() $\mathrm {CAT(0)}$
triangle complexes using a link condition. In [Reference Ballmann and BuyaloBB96, Theorem 7.1], this was proved only for locally compact triangle complexes, and in [Reference Bridson and HaefligerBH99, II.5.2], only for piecewise Euclidean and piecewise hyperbolic triangle complexes.
$\mathrm {CAT(0)}$
triangle complexes using a link condition. In [Reference Ballmann and BuyaloBB96, Theorem 7.1], this was proved only for locally compact triangle complexes, and in [Reference Bridson and HaefligerBH99, II.5.2], only for piecewise Euclidean and piecewise hyperbolic triangle complexes.
Theorem E. A triangle complex X is locally
![]() $\mathrm {CAT}(0)$
if and only if
$\mathrm {CAT}(0)$
if and only if
-
(i) the Gaussian curvature of
 $\sigma _T$
at any interior point of a triangle T of X is
$\sigma _T$
at any interior point of a triangle T of X is
 $\leq 0$
, and
$\leq 0$
, and -
(ii) the sum of geodesic curvatures in any two distinct triangles of X at any interior point of a common edge is
 $\leq 0$
and
$\leq 0$
and -
(iii) for each vertex v of X, the girth of the link
 $\mathrm {lk}^X_v$
is
$\mathrm {lk}^X_v$
is
 $\geq 2\pi $
.
$\geq 2\pi $
.
Motivation and relation to other results
The term Tits Alternative usually refers to the property that all finitely generated subgroups either are virtually solvable or contain a nonabelian free group. The name comes from the theorem of Tits [Reference TitsTit72], who proved that every finitely generated linear group either is virtually solvable or contains a nonabelian free group. It is widely believed (see, e.g. [Reference BestvinaBes00, Question 2.8], [Reference BridsonBri06], [Reference BridsonBri07, Question 7.1], [Reference Farb, Hruska and ThomasFHT11, Problem 12], [Reference CapraceCap14, Section 5]) that all
![]() $\mathrm {CAT(0)}$
groups (groups acting geometrically, that is, properly and cocompactly, on
$\mathrm {CAT(0)}$
groups (groups acting geometrically, that is, properly and cocompactly, on
![]() $\mathrm {CAT(0)}$
spaces) satisfy the Tits Alternative. This was proved only in a limited number of cases (see [Reference Noskov and VinbergNV02, Reference Sageev and WiseSW05, Reference Caprace and SageevCS11, Reference Martin and PrzytyckiMP20, Reference Martin and PrzytyckiMP22, Reference Osajda and PrzytyckiOP21] and references therein). Groups acting geometrically on
$\mathrm {CAT(0)}$
spaces) satisfy the Tits Alternative. This was proved only in a limited number of cases (see [Reference Noskov and VinbergNV02, Reference Sageev and WiseSW05, Reference Caprace and SageevCS11, Reference Martin and PrzytyckiMP20, Reference Martin and PrzytyckiMP22, Reference Osajda and PrzytyckiOP21] and references therein). Groups acting geometrically on
![]() $2$
-dimensional
$2$
-dimensional
![]() $\mathrm {CAT(0)}$
complexes were studied thoroughly by Ballmann and Brin in [Reference Ballmann and BrinBB95], where they proved the Rank Rigidity Conjecture for such groups. They also proved that such groups either are virtually abelian, or they contain a nonabelian free group (statements of this type are sometimes called the Weak Tits Alternative [Reference Sageev and WiseSW05]). However, the Tits Alternative for such groups has been open till our current work (e.g. in [Reference Farb, Hruska and ThomasFHT11, Problem 12] the question on the Tits Alternative is asked specifically in dimension
$\mathrm {CAT(0)}$
complexes were studied thoroughly by Ballmann and Brin in [Reference Ballmann and BrinBB95], where they proved the Rank Rigidity Conjecture for such groups. They also proved that such groups either are virtually abelian, or they contain a nonabelian free group (statements of this type are sometimes called the Weak Tits Alternative [Reference Sageev and WiseSW05]). However, the Tits Alternative for such groups has been open till our current work (e.g. in [Reference Farb, Hruska and ThomasFHT11, Problem 12] the question on the Tits Alternative is asked specifically in dimension
![]() $2$
). Just recently, together with Norin, we were able to show in [Reference Norin, Osajda and PrzytyckiNOP22], among other results, that the groups in question do not contain infinite torsion subgroups. This property might be seen as the first step towards the Tits Alternative. In [Reference Osajda and PrzytyckiOP21], we proved the Tits Alternative for the class of
$2$
). Just recently, together with Norin, we were able to show in [Reference Norin, Osajda and PrzytyckiNOP22], among other results, that the groups in question do not contain infinite torsion subgroups. This property might be seen as the first step towards the Tits Alternative. In [Reference Osajda and PrzytyckiOP21], we proved the Tits Alternative for the class of
![]() $2$
-dimensional recurrent complexes. This class contains all
$2$
-dimensional recurrent complexes. This class contains all
![]() $2$
-dimensional Euclidean buildings,
$2$
-dimensional Euclidean buildings,
![]() $2$
-dimensional systolic complexes, as well as some complexes outside the
$2$
-dimensional systolic complexes, as well as some complexes outside the
![]() $\mathrm {CAT(0)}$
setting.
$\mathrm {CAT(0)}$
setting.
Regarding Corollary C, for right-angled Artin groups, the Tits Alternative follows from the work of Baudisch [Reference BaudischBau81]. In our previous work [Reference Osajda and PrzytyckiOP21], we showed the Tits Alternative for a subclass of
![]() $2$
-dimensional Artin groups, containing all large-type Artin groups. Recently, in [Reference Martin and PrzytyckiMP22], we proved the Tits Alternative for
$2$
-dimensional Artin groups, containing all large-type Artin groups. Recently, in [Reference Martin and PrzytyckiMP22], we proved the Tits Alternative for
![]() $2$
-dimensional Artin groups of hyperbolic type, and in [Reference Martin and PrzytyckiMP20], we proved it for FC-type Artin groups. An approach to the Tits Alternative for subgroups of
$2$
-dimensional Artin groups of hyperbolic type, and in [Reference Martin and PrzytyckiMP20], we proved it for FC-type Artin groups. An approach to the Tits Alternative for subgroups of
![]() $2$
-dimensional Artin groups acting not almost freely on the modified Deligne complex has been developed by Martin [Reference MartinMar22]. As for Corollary D, Cantat proved that the group of birational transformations
$2$
-dimensional Artin groups acting not almost freely on the modified Deligne complex has been developed by Martin [Reference MartinMar22]. As for Corollary D, Cantat proved that the group of birational transformations
![]() $\mathrm {Bir}(\mathbb {C}^2)$
satisfies the Tits Alternative [Reference CantatCan11]. Earlier, Lamy proved the Tits Alternative for the group of polynomial automorphisms
$\mathrm {Bir}(\mathbb {C}^2)$
satisfies the Tits Alternative [Reference CantatCan11]. Earlier, Lamy proved the Tits Alternative for the group of polynomial automorphisms
![]() $\mathrm {Aut}(\mathbb {C}^2)$
[Reference LamyLam01]. These proofs extend to any field
$\mathrm {Aut}(\mathbb {C}^2)$
[Reference LamyLam01]. These proofs extend to any field
![]() $\textbf k$
of characteristic
$\textbf k$
of characteristic
![]() $0$
[Reference LamyLam22]. The same statement for
$0$
[Reference LamyLam22]. The same statement for
![]() $\mathrm {Aut}(\textbf k^3)$
seems at the moment out of reach, since there is no analogue for
$\mathrm {Aut}(\textbf k^3)$
seems at the moment out of reach, since there is no analogue for
![]() $\mathrm {Aut}(\textbf k^3)$
of the
$\mathrm {Aut}(\textbf k^3)$
of the
![]() $\mathrm {CAT(0)}$
complex
$\mathrm {CAT(0)}$
complex
![]() $\textbf {X}$
from [Reference Lamy and PrzytyckiLP21]. However, we believe that for
$\textbf {X}$
from [Reference Lamy and PrzytyckiLP21]. However, we believe that for
![]() $\mathrm {Tame}(\textbf k^3)\lneq \mathrm {Aut}(\textbf k^3)$
, with
$\mathrm {Tame}(\textbf k^3)\lneq \mathrm {Aut}(\textbf k^3)$
, with
![]() $\textbf k$
of characteristic
$\textbf k$
of characteristic
![]() $0$
, one could study the subgroups acting not almost freely on
$0$
, one could study the subgroups acting not almost freely on
![]() $\textbf {X}$
by generalising the methods of the current paper.Footnote 1
$\textbf {X}$
by generalising the methods of the current paper.Footnote 1
One of the main obstacles to generalising Theorem A to higher-dimensional complexes lies in the proof of Proposition 3.1, where it is used that the fundamental groups of graphs are free, whereas the fundamental groups of higher-dimensional complexes can be arbitrary.
Finally, note that assuming in Theorem A that X is locally compact would allow us to avoid proving Theorem E, but otherwise it would not simplify the proof.
Organisation
In Section 2, we prove Theorem E. In Section 3, we recall the method of invariant cocompact subcomplexes from [Reference Osajda and PrzytyckiOP21], which allows us to reduce Theorem A to Proposition 3.2 that assumes the existence of edges of degree
![]() $\geq 3$
in our complex X. Under this assumption, we can exclude the cases of virtually cyclic or
$\geq 3$
in our complex X. Under this assumption, we can exclude the cases of virtually cyclic or
![]() $\mathbb {Z}^2$
groups in Section 4. In technical Section 5, which we recommend to skip at the first reading, we arrange our complex X to have no ‘unfoldable’ links.Footnote 2 We give criteria for finding ‘rank 1’ elements, and consequently free subgroups, in Section 6. In the absence of ‘rank 1’ elements, we obtain a particular rationality property of the complex X in Section 7. In Section 8, we give new criteria for distinguishing the endpoints of certain piecewise geodesics. Together with a Poincaré recurrence argument, this allows us to prove Proposition 3.2 in Section 9.
$\mathbb {Z}^2$
groups in Section 4. In technical Section 5, which we recommend to skip at the first reading, we arrange our complex X to have no ‘unfoldable’ links.Footnote 2 We give criteria for finding ‘rank 1’ elements, and consequently free subgroups, in Section 6. In the absence of ‘rank 1’ elements, we obtain a particular rationality property of the complex X in Section 7. In Section 8, we give new criteria for distinguishing the endpoints of certain piecewise geodesics. Together with a Poincaré recurrence argument, this allows us to prove Proposition 3.2 in Section 9.
2 Characterisation of
 $\mathrm {CAT}(0)$
triangle complexes
$\mathrm {CAT}(0)$
triangle complexes
In this section, we prove Theorem E, which characterises
![]() $\mathrm {CAT}(0)$
triangle complexes. The following result is known under the name of the Cartan–Hadamard theorem.
$\mathrm {CAT}(0)$
triangle complexes. The following result is known under the name of the Cartan–Hadamard theorem.
Theorem 2.1 [Reference Bridson and HaefligerBH99, II.4.1(2)]
Let X be a complete connected metric space. If X is simply connected and locally
![]() $\mathrm {CAT}(0)$
, then it is
$\mathrm {CAT}(0)$
, then it is
![]() $\mathrm {CAT}(0)$
.
$\mathrm {CAT}(0)$
.
We also have the following consequence of [Reference Bridson and HaefligerBH99, II.1.7(4) and II.4.14(2)].
Theorem 2.2. Let X be a complete
![]() $\mathrm {CAT}(0)$
space. A piecewise local geodesic in X with Alexandrov angles
$\mathrm {CAT}(0)$
space. A piecewise local geodesic in X with Alexandrov angles
![]() $\pi $
at the breakpoints is a geodesic.
$\pi $
at the breakpoints is a geodesic.
Let x be a point of a triangle complex X. Let
![]() $\mathrm {lk}^X_x$
be the metric graph that is the link of x, as defined in [Reference Ballmann and BrinBB95, page 176]. Namely, if x is a vertex of X, then the vertices of
$\mathrm {lk}^X_x$
be the metric graph that is the link of x, as defined in [Reference Ballmann and BrinBB95, page 176]. Namely, if x is a vertex of X, then the vertices of
![]() $\mathrm {lk}^X_x$
correspond to the edges of X containing x, and the edges of
$\mathrm {lk}^X_x$
correspond to the edges of X containing x, and the edges of
![]() $\mathrm {lk}^X_x$
correspond to the triangles of X containing x. The length of each edge is the angle in the corresponding triangle of X. Since we assumed that triangles containing x belong to only finitely many isometry classes of
$\mathrm {lk}^X_x$
correspond to the triangles of X containing x. The length of each edge is the angle in the corresponding triangle of X. Since we assumed that triangles containing x belong to only finitely many isometry classes of
![]() $\sigma _T$
, there are only finitely many possible edge lengths in a given
$\sigma _T$
, there are only finitely many possible edge lengths in a given
![]() $\mathrm {lk}^X_x$
. If x lies in the interior of an edge e of X, then
$\mathrm {lk}^X_x$
. If x lies in the interior of an edge e of X, then
![]() $\mathrm {lk}^X_x$
has two vertices corresponding to the components of
$\mathrm {lk}^X_x$
has two vertices corresponding to the components of
![]() $e\setminus x$
, and edges of length
$e\setminus x$
, and edges of length
![]() $\pi $
corresponding to the triangles of X containing e. If x lies in the interior of a triangle, then
$\pi $
corresponding to the triangles of X containing e. If x lies in the interior of a triangle, then
![]() $\mathrm {lk}^X_x$
is a circle of length
$\mathrm {lk}^X_x$
is a circle of length
![]() $2\pi $
. We denote by
$2\pi $
. We denote by
![]() $d_x^X$
(or, shortly,
$d_x^X$
(or, shortly,
![]() $d_x$
) the length metric on
$d_x$
) the length metric on
![]() $\mathrm {lk}_x^X$
. By [Reference Norin, Osajda and PrzytyckiNOP22, Lemma 2.1], we can identify
$\mathrm {lk}_x^X$
. By [Reference Norin, Osajda and PrzytyckiNOP22, Lemma 2.1], we can identify
![]() $\mathrm {lk}^X_x$
with the completion of the space of directions at x (see [Reference Bridson and HaefligerBH99, II.3.18]). Thus, a local geodesic in X starting at x determines a point in
$\mathrm {lk}^X_x$
with the completion of the space of directions at x (see [Reference Bridson and HaefligerBH99, II.3.18]). Thus, a local geodesic in X starting at x determines a point in
![]() $\mathrm {lk}^X_x$
. The angle at x between two such local geodesics is defined to be the distance between the two corresponding points in
$\mathrm {lk}^X_x$
. The angle at x between two such local geodesics is defined to be the distance between the two corresponding points in
![]() $\mathrm {lk}^X_x$
with respect to the metric
$\mathrm {lk}^X_x$
with respect to the metric
![]() $d_x$
. By [Reference Norin, Osajda and PrzytyckiNOP22, Lemma 2.1], if this angle is
$d_x$
. By [Reference Norin, Osajda and PrzytyckiNOP22, Lemma 2.1], if this angle is
![]() $<\pi $
, then it coincides with the Alexandrov angle, and if it is
$<\pi $
, then it coincides with the Alexandrov angle, and if it is
![]() $\geq \pi $
, then the Alexandrov angle equals
$\geq \pi $
, then the Alexandrov angle equals
![]() $\pi $
.
$\pi $
.
Proof of Theorem E
In the ‘only if’ part, condition (i) follows from [Reference Bridson and HaefligerBH99, II.1A.6]. The proof of condition (ii) is identical to that in [Reference Ballmann and BuyaloBB96, Theorem 7.1], and the proof of condition (iii) was given in [Reference Norin, Osajda and PrzytyckiNOP22, Section 2]. For the proof of the ‘if’ part, suppose that a triangle complex X satisfies conditions (i)–(iii). By condition (i) and [Reference Bridson and HaefligerBH99, II.1A.6], we have that X is locally
![]() $\mathrm {CAT}(0)$
at any interior point of a triangle.
$\mathrm {CAT}(0)$
at any interior point of a triangle.
Consider now an edge e of X. Let
![]() $\mathrm {St}(e)$
be the union of all the closed triangles containing e. We will show that
$\mathrm {St}(e)$
be the union of all the closed triangles containing e. We will show that
![]() $\mathrm {St}(e)$
is
$\mathrm {St}(e)$
is
![]() $\mathrm {CAT}(0)$
, which implies that X is locally
$\mathrm {CAT}(0)$
, which implies that X is locally
![]() $\mathrm {CAT}(0)$
at any interior point x of e, since the metrics on
$\mathrm {CAT}(0)$
at any interior point x of e, since the metrics on
![]() $\mathrm {St}(e)$
and on X coincide on a sufficiently small neighbourhood of x. Let
$\mathrm {St}(e)$
and on X coincide on a sufficiently small neighbourhood of x. Let
![]() $Y\subset \mathrm {St}(e)$
be the union of the triangles T for which there exists a point on e with positive geodesic curvature in T. By condition (ii), there is at most one such triangle of given isometry type
$Y\subset \mathrm {St}(e)$
be the union of the triangles T for which there exists a point on e with positive geodesic curvature in T. By condition (ii), there is at most one such triangle of given isometry type
![]() $T_0$
and given embedding
$T_0$
and given embedding
![]() $e\subset T_0$
, so Y has finitely many triangles. We denote this number by
$e\subset T_0$
, so Y has finitely many triangles. We denote this number by
![]() $m(e)$
for future reference. For each triangle T of
$m(e)$
for future reference. For each triangle T of
![]() $\mathrm {St}(e)$
outside Y, denote
$\mathrm {St}(e)$
outside Y, denote
![]() $Y_T=Y\cup T$
. By conditions (i) and (ii), and by [Reference Ballmann and BuyaloBB96, Theorem 7.1], we have that each
$Y_T=Y\cup T$
. By conditions (i) and (ii), and by [Reference Ballmann and BuyaloBB96, Theorem 7.1], we have that each
![]() $Y_T$
is locally
$Y_T$
is locally
![]() $\mathrm {CAT}(0)$
, hence,
$\mathrm {CAT}(0)$
, hence,
![]() $\mathrm {CAT}(0)$
by Theorem 2.1 (note that a geodesic in
$\mathrm {CAT}(0)$
by Theorem 2.1 (note that a geodesic in
![]() $Y_T$
might enter and exit a given triangle infinitely many times). Furthermore, the inclusion
$Y_T$
might enter and exit a given triangle infinitely many times). Furthermore, the inclusion
![]() $Y\subset Y_T$
is an isometric embedding, since points of e have nonpositive geodesic curvature in T. By [Reference Bridson and HaefligerBH99, II.11.3], the union
$Y\subset Y_T$
is an isometric embedding, since points of e have nonpositive geodesic curvature in T. By [Reference Bridson and HaefligerBH99, II.11.3], the union
![]() $\mathrm {St}(e)$
of
$\mathrm {St}(e)$
of
![]() $Y_T$
is
$Y_T$
is
![]() $\mathrm {CAT}(0)$
, as desired.
$\mathrm {CAT}(0)$
, as desired.
Consider now a vertex v of X. After possibly subdividing X, we can assume that in each triangle T containing v, the local geodesic
![]() $\gamma _T$
starting at v and bisecting the angle of T at v ends at the opposite side of T. We will prove that the union
$\gamma _T$
starting at v and bisecting the angle of T at v ends at the opposite side of T. We will prove that the union
![]() $\mathrm {St}(v)$
of all the closed triangles and edges containing v is
$\mathrm {St}(v)$
of all the closed triangles and edges containing v is
![]() $\mathrm {CAT}(0)$
. This will imply that X is locally
$\mathrm {CAT}(0)$
. This will imply that X is locally
![]() $\mathrm {CAT}(0)$
at v, since the metrics on
$\mathrm {CAT}(0)$
at v, since the metrics on
![]() $\mathrm {St}(v)$
and on X coincide on a sufficiently small neighbourhood of v.
$\mathrm {St}(v)$
and on X coincide on a sufficiently small neighbourhood of v.
Claim.
![]() $\mathrm {St}(v)$
is geodesic, and there is
$\mathrm {St}(v)$
is geodesic, and there is
![]() $M>0$
, such that each geodesic in
$M>0$
, such that each geodesic in
![]() $\mathrm {St}(v)$
intersects the interiors of at most M triangles.
$\mathrm {St}(v)$
intersects the interiors of at most M triangles.
To justify the Claim, we employ the idea of a taut string [Reference Bridson and HaefligerBH99, Chapter I.7.20]. Let
![]() $\theta $
be the minimum of
$\theta $
be the minimum of
![]() $\pi $
and the minimum length of an edge in
$\pi $
and the minimum length of an edge in
![]() $\mathrm {lk}_v^X$
, and set
$\mathrm {lk}_v^X$
, and set
![]() $N=2+\frac {\pi }{\theta }$
. Let
$N=2+\frac {\pi }{\theta }$
. Let
![]() $M=1+ N(1+\max _e m(e))$
, where
$M=1+ N(1+\max _e m(e))$
, where
![]() $m(e)$
is defined as above and the maximum is taken over all the edges e of
$m(e)$
is defined as above and the maximum is taken over all the edges e of
![]() $\mathrm {St}(v)$
containing v. For each such edge e, let
$\mathrm {St}(v)$
containing v. For each such edge e, let
![]() $\mathrm {St}'(e)\subset \mathrm {St}(e)$
be the closure of the component containing e of
$\mathrm {St}'(e)\subset \mathrm {St}(e)$
be the closure of the component containing e of
![]() $\mathrm {St}(e)\setminus \bigcup _{T\subset \mathrm {St}(e)}\gamma _T$
, for
$\mathrm {St}(e)\setminus \bigcup _{T\subset \mathrm {St}(e)}\gamma _T$
, for
![]() $\gamma _T$
as above. Since
$\gamma _T$
as above. Since
![]() $\mathrm {St}'(e)$
is convex in
$\mathrm {St}'(e)$
is convex in
![]() $\mathrm {St}(e)$
, it is
$\mathrm {St}(e)$
, it is
![]() $\mathrm {CAT}(0)$
[Reference Bridson and HaefligerBH99, II.1.15(1)].
$\mathrm {CAT}(0)$
[Reference Bridson and HaefligerBH99, II.1.15(1)].
For
![]() $x,y\in \mathrm {St}(v)$
, a string between x and y is a sequence of edges
$x,y\in \mathrm {St}(v)$
, a string between x and y is a sequence of edges
![]() $e_1,\ldots , e_n$
of
$e_1,\ldots , e_n$
of
![]() $\mathrm {St}(v)$
containing v and points
$\mathrm {St}(v)$
containing v and points
![]() $x_0=x,x_1,\ldots , x_n=y$
with
$x_0=x,x_1,\ldots , x_n=y$
with
![]() $\mathrm {St}'(e_i)$
containing both
$\mathrm {St}'(e_i)$
containing both
![]() $x_{i-1}$
and
$x_{i-1}$
and
![]() $x_i$
. The length of the string is the sum
$x_i$
. The length of the string is the sum
![]() $\Sigma _{i=1}^nd_i(x_{i-1},x_i)$
, where
$\Sigma _{i=1}^nd_i(x_{i-1},x_i)$
, where
![]() $d_i$
is the metric on
$d_i$
is the metric on
![]() $\mathrm {St}'(e_i)$
. The distance between x and y in
$\mathrm {St}'(e_i)$
. The distance between x and y in
![]() $\mathrm {St}(v)$
is the infimum of the lengths of strings between x and y. A string is taut, if
$\mathrm {St}(v)$
is the infimum of the lengths of strings between x and y. A string is taut, if
![]() $n\leq 2$
, or
$n\leq 2$
, or
-
• for each
 $0\leq i\leq n,$
the point
$0\leq i\leq n,$
the point
 $x_i$
is distinct from v, and
$x_i$
is distinct from v, and -
• for each
 $0<i<n,$
the point
$0<i<n,$
the point
 $x_i$
belongs to one of the
$x_i$
belongs to one of the
 $\gamma _T$
defined above and
$\gamma _T$
defined above and -
• for each
 $0<i<n,$
the concatenation of geodesics
$0<i<n,$
the concatenation of geodesics
 $x_{i-1}x_i$
in
$x_{i-1}x_i$
in
 $\mathrm {St}'(e_i)$
and
$\mathrm {St}'(e_i)$
and
 $x_{i}x_{i+1}$
in
$x_{i}x_{i+1}$
in
 $\mathrm {St}'(e_{i+1})$
is a geodesic in
$\mathrm {St}'(e_{i+1})$
is a geodesic in
 $\mathrm {St}'(e_i)\cup \mathrm {St}'(e_{i+1})$
.
$\mathrm {St}'(e_i)\cup \mathrm {St}'(e_{i+1})$
.
We now justify that for each string
![]() $(e_i),(x_i)$
between x and y, we can find a taut string between x and y whose length does not exceed the length of
$(e_i),(x_i)$
between x and y, we can find a taut string between x and y whose length does not exceed the length of
![]() $(e_i),(x_i)$
. Indeed, by discarding some
$(e_i),(x_i)$
. Indeed, by discarding some
![]() $x_i$
, we can first assume that consecutive
$x_i$
, we can first assume that consecutive
![]() $e_i$
are distinct, and so for each
$e_i$
are distinct, and so for each
![]() $0<i<n$
, the point
$0<i<n$
, the point
![]() $x_i$
belongs to one of the
$x_i$
belongs to one of the
![]() $\gamma _T$
. Since
$\gamma _T$
. Since
![]() $\gamma _T$
are compact, there is a choice of
$\gamma _T$
are compact, there is a choice of
![]() $x^{\prime }_i$
in the same
$x^{\prime }_i$
in the same
![]() $\gamma _T$
as
$\gamma _T$
as
![]() $x_i$
, minimising the length of the string
$x_i$
, minimising the length of the string
![]() $(e_i),(x^{\prime }_i)$
. Then the concatenation of geodesics
$(e_i),(x^{\prime }_i)$
. Then the concatenation of geodesics
![]() $x^{\prime }_{i-1}x^{\prime }_i$
in
$x^{\prime }_{i-1}x^{\prime }_i$
in
![]() $\mathrm {St}'(e_i)$
and
$\mathrm {St}'(e_i)$
and
![]() $x^{\prime }_{i}x^{\prime }_{i+1}$
in
$x^{\prime }_{i}x^{\prime }_{i+1}$
in
![]() $\mathrm {St}'(e_{i+1})$
is a geodesic in
$\mathrm {St}'(e_{i+1})$
is a geodesic in
![]() $\mathrm {St}'(e_i)\cup \mathrm {St}'(e_{i+1})$
. Finally, if an
$\mathrm {St}'(e_i)\cup \mathrm {St}'(e_{i+1})$
. Finally, if an
![]() $x^{\prime }_{i-1}$
equals v, and
$x^{\prime }_{i-1}$
equals v, and
![]() $x^{\prime }_{i}\neq x_n$
, then for
$x^{\prime }_{i}\neq x_n$
, then for
![]() $x^{\prime }_i\in \gamma _T$
, the subpath of
$x^{\prime }_i\in \gamma _T$
, the subpath of
![]() $\gamma _T$
from
$\gamma _T$
from
![]() $x^{\prime }_{i-1}$
to
$x^{\prime }_{i-1}$
to
![]() $x^{\prime }_{i}$
is a geodesic in both
$x^{\prime }_{i}$
is a geodesic in both
![]() $\mathrm {St}'(e_i)$
and
$\mathrm {St}'(e_i)$
and
![]() $\mathrm {St}'(e_{i+1})$
, and consequently, we can discard
$\mathrm {St}'(e_{i+1})$
, and consequently, we can discard
![]() $x^{\prime }_{i}$
and
$x^{\prime }_{i}$
and
![]() $e_i$
from the string. Repeating the argument, we arrive at
$e_i$
from the string. Repeating the argument, we arrive at
![]() $i-1=n-1$
or
$i-1=n-1$
or
![]() $i-1=n$
. Analogously, we obtain
$i-1=n$
. Analogously, we obtain
![]() $i-1=1$
or
$i-1=1$
or
![]() $i-1=0$
, and so
$i-1=0$
, and so
![]() $n\leq 2$
.
$n\leq 2$
.
We will now show that a taut string satisfies
![]() $n\leq N$
. We can assume
$n\leq N$
. We can assume
![]() $n>2$
, and so none of
$n>2$
, and so none of
![]() $x_i$
equals v. For
$x_i$
equals v. For
![]() $0<i<n,$
let
$0<i<n,$
let
![]() $\theta _i$
be the Alexandrov angle at
$\theta _i$
be the Alexandrov angle at
![]() $x_{i}$
in
$x_{i}$
in
![]() $\mathrm {St}'(e_{i+1})$
between the geodesics
$\mathrm {St}'(e_{i+1})$
between the geodesics
![]() $x_{i}x_{i+1}$
and
$x_{i}x_{i+1}$
and
![]() $x_{i}v$
. The concatenation of geodesics
$x_{i}v$
. The concatenation of geodesics
![]() $x_{i-1}x_i$
in
$x_{i-1}x_i$
in
![]() $\mathrm {St}'(e_i)$
and
$\mathrm {St}'(e_i)$
and
![]() $x_{i}x_{i+1}$
in
$x_{i}x_{i+1}$
in
![]() $\mathrm {St}'(e_{i+1})$
is a geodesic in
$\mathrm {St}'(e_{i+1})$
is a geodesic in
![]() $\mathrm {St}'(e_i)\cup \mathrm {St}'(e_{i+1})$
, which is
$\mathrm {St}'(e_i)\cup \mathrm {St}'(e_{i+1})$
, which is
![]() $\mathrm {CAT}(0)$
by [Reference Bridson and HaefligerBH99, II.11.3]. Consequently, by the definition of
$\mathrm {CAT}(0)$
by [Reference Bridson and HaefligerBH99, II.11.3]. Consequently, by the definition of
![]() $\theta $
, we have
$\theta $
, we have
![]() $\theta _i\geq \theta _{i-1}+\theta $
. Thus,
$\theta _i\geq \theta _{i-1}+\theta $
. Thus,
![]() $\pi \geq \theta _{n-1}\geq (n-2)\theta +\theta _1$
, and so,
$\pi \geq \theta _{n-1}\geq (n-2)\theta +\theta _1$
, and so,
![]() $n-2\leq \frac {\pi }{\theta }=N-2$
.
$n-2\leq \frac {\pi }{\theta }=N-2$
.
Since there are finitely many isometry types of simplices in
![]() $\mathrm {St}(v)$
, and each taut string satisfies
$\mathrm {St}(v)$
, and each taut string satisfies
![]() $n\leq N$
, the distance between x and y in
$n\leq N$
, the distance between x and y in
![]() $\mathrm {St}(v)$
is realised by the length of some taut string
$\mathrm {St}(v)$
is realised by the length of some taut string
![]() $(e_i),(x_i)$
. Then the concatenation of all the geodesics
$(e_i),(x_i)$
. Then the concatenation of all the geodesics
![]() $x_{i-1}x_i$
in
$x_{i-1}x_i$
in
![]() $\mathrm {St}'(e_i)$
is a geodesic between x and y, proving that
$\mathrm {St}'(e_i)$
is a geodesic between x and y, proving that
![]() $\mathrm {St}(v)$
is geodesic. Furthermore, for any geodesic
$\mathrm {St}(v)$
is geodesic. Furthermore, for any geodesic
![]() $\gamma $
from x to y in
$\gamma $
from x to y in
![]() $\mathrm {St}(v)$
, one can choose points on
$\mathrm {St}(v)$
, one can choose points on
![]() $\gamma $
forming a taut string. Since any taut string satisfies
$\gamma $
forming a taut string. Since any taut string satisfies
![]() $n\leq N$
, and we have that
$n\leq N$
, and we have that
![]() $\gamma $
intersects the interiors of at most
$\gamma $
intersects the interiors of at most
![]() $1+n(1+\max _e m(e))$
triangles, the Claim follows.
$1+n(1+\max _e m(e))$
triangles, the Claim follows.
Returning to the proof of Theorem E, we follow the scheme in [Reference Ballmann and BuyaloBB96, Theorem 7.1] to find a sequence of
![]() $\mathrm {CAT}(0)$
spaces Gromov–Hausdorff converging to
$\mathrm {CAT}(0)$
spaces Gromov–Hausdorff converging to
![]() $\mathrm {St}(v)$
. Namely, realise each (isometry type of a) triangle T of
$\mathrm {St}(v)$
. Namely, realise each (isometry type of a) triangle T of
![]() $\mathrm {St}(v)$
as
$\mathrm {St}(v)$
as
![]() $T\subset \mathbb {R}^2$
, with metric induced from some smooth Riemannian metric of nonpositive Gaussian curvature on
$T\subset \mathbb {R}^2$
, with metric induced from some smooth Riemannian metric of nonpositive Gaussian curvature on
![]() $\mathbb {R}^2$
defined in a neighbourhood U of T. Denote by
$\mathbb {R}^2$
defined in a neighbourhood U of T. Denote by
![]() $e,f$
the edges of T containing v and by g the remaining edge of T. Let l denote the length of e. For each
$e,f$
the edges of T containing v and by g the remaining edge of T. Let l denote the length of e. For each
![]() $n>0$
, we decompose e into paths
$n>0$
, we decompose e into paths
![]() $a^1\cdot a^2 \cdots a^n$
of length
$a^1\cdot a^2 \cdots a^n$
of length
![]() $\frac {l}{n}$
, and we define
$\frac {l}{n}$
, and we define
![]() $\kappa ^k$
to be the integral of the geodesic curvature along
$\kappa ^k$
to be the integral of the geodesic curvature along
![]() $a^k$
. Let
$a^k$
. Let
![]() $e_n$
be the piecewise geodesic in U that starts at v tangent to e, has n locally geodesic pieces of length
$e_n$
be the piecewise geodesic in U that starts at v tangent to e, has n locally geodesic pieces of length
![]() $\frac {l}{n}$
and exterior angle at the k-th breakpoint that equals
$\frac {l}{n}$
and exterior angle at the k-th breakpoint that equals
![]() $\kappa ^k$
. For n sufficiently large the path
$\kappa ^k$
. For n sufficiently large the path
![]() $e_n$
exists, and they
$e_n$
exists, and they
![]() $C^1$
-converge to e as n tends to
$C^1$
-converge to e as n tends to
![]() $\infty $
. We define paths
$\infty $
. We define paths
![]() $f_n$
analogously. We define
$f_n$
analogously. We define
![]() $g_n$
to be any piecewise geodesics joining the endpoints of
$g_n$
to be any piecewise geodesics joining the endpoints of
![]() $e_n$
and
$e_n$
and
![]() $f_n$
and
$f_n$
and
![]() $C^1$
-converging to g. This gives us a triangle
$C^1$
-converging to g. This gives us a triangle
![]() $T_n\subset U$
bounded by
$T_n\subset U$
bounded by
![]() $e_n,f_n$
and
$e_n,f_n$
and
![]() $g_n$
, whose boundary is piecewise geodesic (one can pass to a union of triangles with locally geodesic boundary by subdividing). Furthermore, we have a map
$g_n$
, whose boundary is piecewise geodesic (one can pass to a union of triangles with locally geodesic boundary by subdividing). Furthermore, we have a map
![]() $T_n\to T$
, whose restriction to
$T_n\to T$
, whose restriction to
![]() $e_n,f_n$
preserves length and which is bilipschitz with the bilipschitz constant converging to
$e_n,f_n$
preserves length and which is bilipschitz with the bilipschitz constant converging to
![]() $1$
as n tends to
$1$
as n tends to
![]() $\infty $
. Glueing various
$\infty $
. Glueing various
![]() $T_n$
along the sides corresponding to the ones of T that we glued to form
$T_n$
along the sides corresponding to the ones of T that we glued to form
![]() $\mathrm {St}(v)$
yields a triangle complex that we call
$\mathrm {St}(v)$
yields a triangle complex that we call
![]() $\mathrm {St}(v)_n$
. Then
$\mathrm {St}(v)_n$
. Then
![]() $\mathrm {St}(v)$
is a Gromov–Hausdorff limit of
$\mathrm {St}(v)$
is a Gromov–Hausdorff limit of
![]() $\mathrm {St}(v)_n$
. Note that since
$\mathrm {St}(v)_n$
. Note that since
![]() $\mathrm {St}(v)$
satisfied conditions (i)–(iii), we have that
$\mathrm {St}(v)$
satisfied conditions (i)–(iii), we have that
![]() $\mathrm {St}(v)_n$
satisfies conditions (i)–(iii). Since
$\mathrm {St}(v)_n$
satisfies conditions (i)–(iii). Since
![]() $\mathrm {St}(v)_n$
has locally geodesic edges, and is geodesic by the Claim (applied to
$\mathrm {St}(v)_n$
has locally geodesic edges, and is geodesic by the Claim (applied to
![]() $\mathrm {St}(v)_n$
instead of
$\mathrm {St}(v)_n$
instead of
![]() $\mathrm {St}(v)$
), the same proof as for [Reference Ballmann and BuyaloBB96, Theorem 7.1, case 1] shows that
$\mathrm {St}(v)$
), the same proof as for [Reference Ballmann and BuyaloBB96, Theorem 7.1, case 1] shows that
![]() $\mathrm {St}(v)_n$
is locally
$\mathrm {St}(v)_n$
is locally
![]() $\mathrm {CAT}(0)$
, hence,
$\mathrm {CAT}(0)$
, hence,
![]() $\mathrm {CAT}(0)$
by Theorem 2.1. Consequently, by [Reference Bridson and HaefligerBH99, II.3.10], we have that
$\mathrm {CAT}(0)$
by Theorem 2.1. Consequently, by [Reference Bridson and HaefligerBH99, II.3.10], we have that
![]() $\mathrm {St}(v)$
is
$\mathrm {St}(v)$
is
![]() $\mathrm {CAT}(0)$
.
$\mathrm {CAT}(0)$
.
We have the following immediate consequence of Theorem E.
Corollary 2.3. If X is a triangle complex that is locally
![]() $\mathrm {CAT}(0)$
, then all of its subcomplexes are locally
$\mathrm {CAT}(0)$
, then all of its subcomplexes are locally
![]() $\mathrm {CAT}(0)$
.
$\mathrm {CAT}(0)$
.
Note that while we did not apply the Claim to
![]() $\mathrm {St}(v)$
in the proof of Theorem E, it will be used in the following remarks.
$\mathrm {St}(v)$
in the proof of Theorem E, it will be used in the following remarks.
Remark 2.4. Suppose that X is a
![]() $\mathrm {CAT}(0)$
triangle complex with finitely many isometry types of simplices. Then the constant M in the Claim does not depend on v. As in the ‘
$\mathrm {CAT}(0)$
triangle complex with finitely many isometry types of simplices. Then the constant M in the Claim does not depend on v. As in the ‘
![]() $\Psi _n\Rightarrow \Phi _n$
’ part of the proof of [Reference Bridson and HaefligerBH99, Chapter I.7.28], we obtain that for each l there is
$\Psi _n\Rightarrow \Phi _n$
’ part of the proof of [Reference Bridson and HaefligerBH99, Chapter I.7.28], we obtain that for each l there is
![]() $M'>0$
, such that each geodesic in X of length
$M'>0$
, such that each geodesic in X of length
![]() $\leq l$
intersects the interiors of at most
$\leq l$
intersects the interiors of at most
![]() $M'$
simplices. Using this in the place of [Reference BridsonBri99, Lemma 1] in the proof of [Reference BridsonBri99, Lemma 2 and Theorem A], we obtain that every simplicial isometry g of X is semisimple: it fixes a point, or is loxodromic, meaning that there is a geodesic line
$M'$
simplices. Using this in the place of [Reference BridsonBri99, Lemma 1] in the proof of [Reference BridsonBri99, Lemma 2 and Theorem A], we obtain that every simplicial isometry g of X is semisimple: it fixes a point, or is loxodromic, meaning that there is a geodesic line
![]() $\omega $
in X (called an axis), such that g preserves
$\omega $
in X (called an axis), such that g preserves
![]() $\omega $
and acts on it as a nontrivial translation.
$\omega $
and acts on it as a nontrivial translation.
Remark 2.5. Suppose that X is a
![]() $\mathrm {CAT}(0)$
triangle complex with finitely many isometry types of simplices. Then the set of translation lengths of simplicial isometries of X is a discrete subset of
$\mathrm {CAT}(0)$
triangle complex with finitely many isometry types of simplices. Then the set of translation lengths of simplicial isometries of X is a discrete subset of
![]() $[0,\infty )$
, which is proved using the Claim exactly as [Reference BridsonBri99, Proposition]. Similarly, we obtain the following: Let X be a
$[0,\infty )$
, which is proved using the Claim exactly as [Reference BridsonBri99, Proposition]. Similarly, we obtain the following: Let X be a
![]() $\mathrm {CAT}(0)$
triangle complex with a subcomplex Y on which some group of simplicial isometries of X acts coboundedly. Since any metric ball in X intersects finitely many isometry types of simplices, we have that each bounded neighbourhood of Y intersects finitely many isometry types of simplices. Then for each simplicial isometry g of
$\mathrm {CAT}(0)$
triangle complex with a subcomplex Y on which some group of simplicial isometries of X acts coboundedly. Since any metric ball in X intersects finitely many isometry types of simplices, we have that each bounded neighbourhood of Y intersects finitely many isometry types of simplices. Then for each simplicial isometry g of
![]() $X,$
the set
$X,$
the set
![]() $\inf _{y\in Y}d(y,gy)$
attains its infimum, which we denote
$\inf _{y\in Y}d(y,gy)$
attains its infimum, which we denote
![]() $|g|_Y$
. Moreover, the set of
$|g|_Y$
. Moreover, the set of
![]() $|g|_Y$
over all simplicial isometries g of X is a discrete subset of
$|g|_Y$
over all simplicial isometries g of X is a discrete subset of
![]() $[0,\infty )$
.
$[0,\infty )$
.
3 G-cocompact subcomplexes
Let X be a simplicial complex with an action of a group G. We say that a subcomplex
![]() $Z\subset X$
is an invariant cocompact subcomplex with respect to G (shortly, G-c.s.) if Z is G-invariant, and the quotient
$Z\subset X$
is an invariant cocompact subcomplex with respect to G (shortly, G-c.s.) if Z is G-invariant, and the quotient
![]() $Z/G$
is compact. Note that a G-c.s. is not required to be connected.
$Z/G$
is compact. Note that a G-c.s. is not required to be connected.
A
![]() $2$
-dimensional simplicial complex is essential if every edge has degree at least
$2$
-dimensional simplicial complex is essential if every edge has degree at least
![]() $2$
and none of connected components is a single vertex. An essential simplicial complex is thick if it has an edge of degree at least
$2$
and none of connected components is a single vertex. An essential simplicial complex is thick if it has an edge of degree at least
![]() $3$
.
$3$
.
A disc diagram D is a compact contractible simplicial complex with a fixed embedding in
![]() $\mathbb {R}^2$
. Its boundary path is the attaching map of the cell at
$\mathbb {R}^2$
. Its boundary path is the attaching map of the cell at
![]() $\infty $
. If X is a simplicial complex, a disc diagram in X is a nondegenerate simplicial map
$\infty $
. If X is a simplicial complex, a disc diagram in X is a nondegenerate simplicial map
![]() $\varphi \colon D\to X$
, and its boundary path is the composition of the boundary path of D and
$\varphi \colon D\to X$
, and its boundary path is the composition of the boundary path of D and
![]() $\varphi $
. We say that
$\varphi $
. We say that
![]() $\varphi $
is reduced if it maps triangles sharing an edge to two distinct triangles. By [Reference Osajda and PrzytyckiOP21, Remark 3.6], for each contractible closed edge-path
$\varphi $
is reduced if it maps triangles sharing an edge to two distinct triangles. By [Reference Osajda and PrzytyckiOP21, Remark 3.6], for each contractible closed edge-path
![]() $\alpha $
in a simplicial complex X, there is a reduced disc diagram in X with boundary path
$\alpha $
in a simplicial complex X, there is a reduced disc diagram in X with boundary path
![]() $\alpha $
.
$\alpha $
.
A group G acts on a simplicial complex X without inversions if for any
![]() $g\in G$
stabilising a simplex
$g\in G$
stabilising a simplex
![]() $\sigma $
of X, we have that g fixes
$\sigma $
of X, we have that g fixes
![]() $\sigma $
pointwise. More generally, we say that G acts without weak inversions if for each vertex v of X, there is no
$\sigma $
pointwise. More generally, we say that G acts without weak inversions if for each vertex v of X, there is no
![]() $g\in G$
sending v to a distinct vertex in a common edge.
$g\in G$
sending v to a distinct vertex in a common edge.
The first ingredient in our proof of Theorem A is the following earlier result.
Proposition 3.1 [Reference Osajda and PrzytyckiOP21, Proposition 3.7]
Let G be a finitely generated group acting almost freely and without inversions on a simply connected
![]() $2$
-dimensional simplicial complex X that contains no simplicial
$2$
-dimensional simplicial complex X that contains no simplicial
![]() $2$
-spheres. If X contains no thick G-c.s., then G is virtually cyclic, or virtually
$2$
-spheres. If X contains no thick G-c.s., then G is virtually cyclic, or virtually
![]() $\mathbb {Z}^2$
, or it contains a nonabelian free group.
$\mathbb {Z}^2$
, or it contains a nonabelian free group.
The second ingredient in the proof of Theorem A is the following, the proof of which will occupy the present article.
Proposition 3.2. Let G be a group acting almost freely and without weak inversions on a
![]() $\mathrm {CAT}(0)$
triangle complex X that is an increasing union of connected essential G-c.s. If X contains an edge of degree
$\mathrm {CAT}(0)$
triangle complex X that is an increasing union of connected essential G-c.s. If X contains an edge of degree
![]() $\geq 3$
, then G contains a nonabelian free group.
$\geq 3$
, then G contains a nonabelian free group.
We now show how Theorem A follows from these two ingredients.
Proof of Theorem A
By passing to a subdivision (see [Reference Norin, Osajda and PrzytyckiNOP22, Lemma 2.1]), we can assume that G acts without weak inversions. By Proposition 3.1, we can assume that X contains a thick G-c.s.
![]() $Z_1$
. We will prove that G contains a nonabelian free group. By passing to a connected component of
$Z_1$
. We will prove that G contains a nonabelian free group. By passing to a connected component of
![]() $Z_1$
and its stabiliser
$Z_1$
and its stabiliser
![]() $G'$
in G (which is finitely generated, since it acts properly and cocompactly on a connected complex), we can assume that
$G'$
in G (which is finitely generated, since it acts properly and cocompactly on a connected complex), we can assume that
![]() $Z_1$
is connected. If
$Z_1$
is connected. If
![]() $Z_1$
contains a closed edge-path that is not contractible in
$Z_1$
contains a closed edge-path that is not contractible in
![]() $Z_1$
, repeatedly attaching to
$Z_1$
, repeatedly attaching to
![]() $Z_1$
the images of reduced disc diagrams and their G-translates, we obtain an increasing sequence
$Z_1$
the images of reduced disc diagrams and their G-translates, we obtain an increasing sequence
![]() $Z_1\subset Z_2\subset \cdots $
of connected essential G-c.s., such that their union
$Z_1\subset Z_2\subset \cdots $
of connected essential G-c.s., such that their union
![]() $X'$
is simply connected. By Corollary 2.3, we have that
$X'$
is simply connected. By Corollary 2.3, we have that
![]() $X'$
is locally
$X'$
is locally
![]() $\mathrm {CAT}(0)$
, and so
$\mathrm {CAT}(0)$
, and so
![]() $X'$
is
$X'$
is
![]() $\mathrm {CAT}(0)$
by Theorem 2.1. It remains to apply Proposition 3.2.
$\mathrm {CAT}(0)$
by Theorem 2.1. It remains to apply Proposition 3.2.
4 Not virtually cyclic or
 $\mathbb {Z}^2$
$\mathbb {Z}^2$
The first step of the proof of Proposition 3.2 is the following.
Lemma 4.1. Let G be a group acting almost freely on a
![]() $\mathrm {CAT}(0)$
triangle complex X. If X contains a subcomplex Z that is a connected thick G-c.s., then
$\mathrm {CAT}(0)$
triangle complex X. If X contains a subcomplex Z that is a connected thick G-c.s., then
-
(i) G is not virtually cyclic and
-
(ii) G is not virtually
 $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
In the proof of Lemma 4.1, we will need the following vocabulary. Let X be a triangle complex. We say that a ray
![]() $\gamma \colon [0,\infty )\to X$
or a path
$\gamma \colon [0,\infty )\to X$
or a path
![]() $\gamma \colon [0,1]\to X$
starts (respectively, ends) in a simplex
$\gamma \colon [0,1]\to X$
starts (respectively, ends) in a simplex
![]() $\sigma $
, if for some
$\sigma $
, if for some
![]() $\varepsilon>0$
the points
$\varepsilon>0$
the points
![]() $\gamma (0,\varepsilon )$
(respectively,
$\gamma (0,\varepsilon )$
(respectively,
![]() $\gamma (1-\varepsilon ,1)$
) all lie in the interior of
$\gamma (1-\varepsilon ,1)$
) all lie in the interior of
![]() $\sigma $
. If
$\sigma $
. If
![]() $\gamma (0)$
(respectively,
$\gamma (0)$
(respectively,
![]() $\gamma (1)$
) lies in the interior of an edge e, then
$\gamma (1)$
) lies in the interior of an edge e, then
![]() $\gamma $
starts (respectively, ends) perpendicularly to e if the angle at
$\gamma $
starts (respectively, ends) perpendicularly to e if the angle at
![]() $\gamma (0)$
(respectively,
$\gamma (0)$
(respectively,
![]() $\gamma (1)$
) between
$\gamma (1)$
) between
![]() $\gamma $
and e is
$\gamma $
and e is
![]() $\frac {\pi }{2}$
.
$\frac {\pi }{2}$
.
We will also need the following, which generalises an argument in the proof of [Reference Martin and PrzytyckiMP21, Theorem A].
Lemma 4.2. Let A be a group isomorphic to
![]() $\mathbb {Z}^2$
acting freely on a
$\mathbb {Z}^2$
acting freely on a
![]() $\mathrm {CAT}(0)$
triangle complex W with finitely many isometry types of simplices. Then there is an isometrically embedded A-cocompact subcomplex in W isometric to the Euclidean plane.
$\mathrm {CAT}(0)$
triangle complex W with finitely many isometry types of simplices. Then there is an isometrically embedded A-cocompact subcomplex in W isometric to the Euclidean plane.
Proof. Since W has finitely many isometry types of simplices, by Remark 2.4, all elements of A act as loxodromic isometries on W. By [Reference Bridson and HaefligerBH99, II.7.20(1)], we have
![]() $\mathrm {Min}(A) = Y \times \mathbb {R}^n$
with A preserving the product structure and acting trivially on Y. By [Reference Bridson and HaefligerBH99, II.7.20(2)], we have
$\mathrm {Min}(A) = Y \times \mathbb {R}^n$
with A preserving the product structure and acting trivially on Y. By [Reference Bridson and HaefligerBH99, II.7.20(2)], we have
![]() $n\leq 2$
, but since A acts freely by simplicial isometries, we have
$n\leq 2$
, but since A acts freely by simplicial isometries, we have
![]() $n=2$
, and so Y is a point, as desired.
$n=2$
, and so Y is a point, as desired.
Proof of Lemma 4.1
Let e be an edge of Z of degree
![]() $\geq 3$
, and let x be a point in the interior of e. Let
$\geq 3$
, and let x be a point in the interior of e. Let
![]() $b_1,b_2,b_3,$
be geodesics starting at x perpendicularly to e contained in distinct triangles
$b_1,b_2,b_3,$
be geodesics starting at x perpendicularly to e contained in distinct triangles
![]() $T_1,T_2,T_3$
. For each
$T_1,T_2,T_3$
. For each
![]() $i=1,2,3,$
the set of starting directions at points in
$i=1,2,3,$
the set of starting directions at points in
![]() $\partial T_i$
of geodesics intersecting
$\partial T_i$
of geodesics intersecting
![]() $b_i$
at angle
$b_i$
at angle
![]() $<\frac {\pi }{6}$
has positive Liouville measure (see [Reference Ballmann and BrinBB95, Section 3]). Let S denote the union of all the open edges in the links
$<\frac {\pi }{6}$
has positive Liouville measure (see [Reference Ballmann and BrinBB95, Section 3]). Let S denote the union of all the open edges in the links
![]() $\mathrm {lk}_y^Z$
for all
$\mathrm {lk}_y^Z$
for all
![]() $y\in Z^1\setminus Z^0$
, with the (infinite) Liouville measure. We say that
$y\in Z^1\setminus Z^0$
, with the (infinite) Liouville measure. We say that
![]() $(\xi _j)_j\in S^{\mathbb {Z}}$
with
$(\xi _j)_j\in S^{\mathbb {Z}}$
with
![]() $\xi _j\in \mathrm {lk}_{y_j}^Z$
determines a locally geodesic oriented line
$\xi _j\in \mathrm {lk}_{y_j}^Z$
determines a locally geodesic oriented line
![]() $\gamma $
in
$\gamma $
in
![]() $Z\setminus Z^0$
transverse to
$Z\setminus Z^0$
transverse to
![]() $Z^1$
if
$Z^1$
if
![]() $\gamma $
intersects
$\gamma $
intersects
![]() $Z^1$
exactly at points
$Z^1$
exactly at points
![]() $y_j$
in directions
$y_j$
in directions
![]() $\xi _j$
, in that order. Since G acts on Z properly and cocompactly, the set of
$\xi _j$
, in that order. Since G acts on Z properly and cocompactly, the set of
![]() $(\xi _j)_j\in S^{\mathbb {Z}}$
that determine locally geodesic oriented lines projects to a full measure subset in each coordinate S (see [Reference Ballmann and BrinBB95, Section 3], which relies on [Reference Cornfeld, Fomin and SinaĭCFS82, Chapter 6]). Consequently, for
$(\xi _j)_j\in S^{\mathbb {Z}}$
that determine locally geodesic oriented lines projects to a full measure subset in each coordinate S (see [Reference Ballmann and BrinBB95, Section 3], which relies on [Reference Cornfeld, Fomin and SinaĭCFS82, Chapter 6]). Consequently, for
![]() $i=1,2,3,$
there exists a locally geodesic ray
$i=1,2,3,$
there exists a locally geodesic ray
![]() $\gamma _i$
in Z starting at an interior point
$\gamma _i$
in Z starting at an interior point
![]() $x_i$
of
$x_i$
of
![]() $b_i$
at angle
$b_i$
at angle
![]() $<\frac {\pi }{6}$
from
$<\frac {\pi }{6}$
from
![]() $b_i$
, disjoint from
$b_i$
, disjoint from
![]() $Z^0$
and transverse to
$Z^0$
and transverse to
![]() $Z^1$
. Let
$Z^1$
. Let
![]() $a_i=xx_i\subset b_i$
. See Figure 1.
$a_i=xx_i\subset b_i$
. See Figure 1.

Figure 1 The geodesic ray
![]() $\gamma _1$
.
$\gamma _1$
.
Since X is
![]() $\mathrm {CAT}(0)$
, by Theorem 2.2, we have that
$\mathrm {CAT}(0)$
, by Theorem 2.2, we have that
![]() $\gamma _i$
are geodesic rays in X and
$\gamma _i$
are geodesic rays in X and
![]() $a^{-1}_i\cdot a_j$
are geodesics in X. Since each
$a^{-1}_i\cdot a_j$
are geodesics in X. Since each
![]() $\gamma ^{-1}_i\cdot a^{-1}_i\cdot a_j\cdot \gamma _j$
is a piecewise geodesic with angles
$\gamma ^{-1}_i\cdot a^{-1}_i\cdot a_j\cdot \gamma _j$
is a piecewise geodesic with angles
![]() $>\frac {5\pi }{6}$
at the two breakpoints, by [Reference Bridson and HaefligerBH99, II.9.3], the rays
$>\frac {5\pi }{6}$
at the two breakpoints, by [Reference Bridson and HaefligerBH99, II.9.3], the rays
![]() $\gamma _i,\gamma _j$
are not asymptotic and they determine points at distance
$\gamma _i,\gamma _j$
are not asymptotic and they determine points at distance
![]() $>\frac {2\pi }{3}$
in the Tits boundary of X. In particular, Z cannot be quasi-isometric to
$>\frac {2\pi }{3}$
in the Tits boundary of X. In particular, Z cannot be quasi-isometric to
![]() $\mathbb {R}$
since it contains three pairwise nonasymptotic geodesic rays. This proves (i).
$\mathbb {R}$
since it contains three pairwise nonasymptotic geodesic rays. This proves (i).
For (ii), assume for contradiction, that G is virtually
![]() $\mathbb {Z}^2$
generated by elements
$\mathbb {Z}^2$
generated by elements
![]() $g,h$
. Let
$g,h$
. Let
![]() $\alpha , \beta $
be edge-paths in Z connecting a basepoint
$\alpha , \beta $
be edge-paths in Z connecting a basepoint
![]() $y\in Z^0$
to
$y\in Z^0$
to
![]() $gy,hy$
, respectively. Then the concatenation
$gy,hy$
, respectively. Then the concatenation
![]() $\alpha \cdot g\beta \cdot h\alpha ^{-1}\cdot \beta ^{-1}$
is a closed edge-path, and since X is simply connected, there is a reduced disc diagram
$\alpha \cdot g\beta \cdot h\alpha ^{-1}\cdot \beta ^{-1}$
is a closed edge-path, and since X is simply connected, there is a reduced disc diagram
![]() $D\to X$
with that boundary path. Let
$D\to X$
with that boundary path. Let
![]() $Z'\subset X$
be the connected thick G-c.s. obtained from Z by adding the translates under G of the image of D. The complex
$Z'\subset X$
be the connected thick G-c.s. obtained from Z by adding the translates under G of the image of D. The complex
![]() $Z'$
is locally
$Z'$
is locally
![]() $\mathrm {CAT}(0)$
by Corollary 2.3. Let
$\mathrm {CAT}(0)$
by Corollary 2.3. Let
![]() $\widetilde Z'\to Z'$
be the universal cover of
$\widetilde Z'\to Z'$
be the universal cover of
![]() $Z'$
, which is
$Z'$
, which is
![]() $\mathrm {CAT}(0)$
by Theorem 2.1. The action of G on
$\mathrm {CAT}(0)$
by Theorem 2.1. The action of G on
![]() $Z'$
lifts to an almost free action of a group
$Z'$
lifts to an almost free action of a group
![]() $\widetilde G$
on
$\widetilde G$
on
![]() $\widetilde Z'$
fitting into the short exact sequence
$\widetilde Z'$
fitting into the short exact sequence
![]() $\pi _1 Z'\to \widetilde G\to G$
. Since
$\pi _1 Z'\to \widetilde G\to G$
. Since
![]() $D\to Z'$
lifts to
$D\to Z'$
lifts to
![]() $D\to \widetilde Z'$
, we have commuting
$D\to \widetilde Z'$
, we have commuting
![]() $\tilde g, \tilde h\in \widetilde G$
mapping to
$\tilde g, \tilde h\in \widetilde G$
mapping to
![]() $g,h\in G$
, and, hence, generating a subgroup
$g,h\in G$
, and, hence, generating a subgroup
![]() $A< \widetilde G$
isomorphic to
$A< \widetilde G$
isomorphic to
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
Since A acts almost freely and is torsion free, we have that it acts freely on
![]() $\widetilde Z'$
. By Lemma 4.2 applied with
$\widetilde Z'$
. By Lemma 4.2 applied with
![]() $W=\widetilde Z'$
, there is an isometrically embedded A-cocompact subcomplex
$W=\widetilde Z'$
, there is an isometrically embedded A-cocompact subcomplex
![]() $E\subset \widetilde Z'$
isometric to the Euclidean plane. We now justify that the composition
$E\subset \widetilde Z'$
isometric to the Euclidean plane. We now justify that the composition
![]() $\phi \colon E\subset \widetilde Z'\to Z'\subset X$
is an isometric embedding.
$\phi \colon E\subset \widetilde Z'\to Z'\subset X$
is an isometric embedding.
Indeed, for two triangles
![]() $T,T'$
of E containing a common edge
$T,T'$
of E containing a common edge
![]() $e'$
, the sum of the geodesic curvatures in
$e'$
, the sum of the geodesic curvatures in
![]() $\phi (T)$
and
$\phi (T)$
and
![]() $\phi (T')$
at any point of
$\phi (T')$
at any point of
![]() $\phi (e')$
equals
$\phi (e')$
equals
![]() $0$
, and so the geodesic curvature at
$0$
, and so the geodesic curvature at
![]() $\phi (e')$
in any triangle of X distinct from
$\phi (e')$
in any triangle of X distinct from
![]() $\phi (T),\phi (T')$
is nonpositive. Consequently,
$\phi (T),\phi (T')$
is nonpositive. Consequently,
![]() $\phi $
is a local isometric embedding at
$\phi $
is a local isometric embedding at
![]() $e'$
. Furthermore, since E is isometric to the Euclidean plane, for any geodesic
$e'$
. Furthermore, since E is isometric to the Euclidean plane, for any geodesic
![]() $\gamma $
in E passing through a vertex v, the angle (see Section 2) between the incoming and outgoing directions of
$\gamma $
in E passing through a vertex v, the angle (see Section 2) between the incoming and outgoing directions of
![]() $\gamma $
at v equals
$\gamma $
at v equals
![]() $\pi $
. Since the map that
$\pi $
. Since the map that
![]() $\phi $
induces between
$\phi $
induces between
![]() $\mathrm {lk}_v^E$
and
$\mathrm {lk}_v^E$
and
![]() $\mathrm {lk}_{\phi (v)}^X$
is locally injective, the angle between the incoming and outgoing directions of
$\mathrm {lk}_{\phi (v)}^X$
is locally injective, the angle between the incoming and outgoing directions of
![]() $\phi (\gamma )$
at
$\phi (\gamma )$
at
![]() $\phi (v)$
equals
$\phi (v)$
equals
![]() $\pi $
as well. By Theorem 2.2, we have that
$\pi $
as well. By Theorem 2.2, we have that
![]() $\phi (\gamma )$
is a geodesic. Thus,
$\phi (\gamma )$
is a geodesic. Thus,
![]() $\phi $
is an isometric embedding, as desired.
$\phi $
is an isometric embedding, as desired.
Since the image of A in G is of finite index, it acts cocompactly on
![]() $Z'$
. Consequently, the geodesic rays
$Z'$
. Consequently, the geodesic rays
![]() $\gamma _i$
from the proof of part (i) are at bounded distance from
$\gamma _i$
from the proof of part (i) are at bounded distance from
![]() $\phi (E)$
in
$\phi (E)$
in
![]() $Z'$
. Since X is
$Z'$
. Since X is
![]() $\mathrm {CAT}(0)$
, we obtain that each
$\mathrm {CAT}(0)$
, we obtain that each
![]() $\gamma _i$
is asymptotic to a geodesic ray in
$\gamma _i$
is asymptotic to a geodesic ray in
![]() $\phi (E)$
and these three rays are pairwise at angle
$\phi (E)$
and these three rays are pairwise at angle
![]() $>\frac {2\pi }{3}$
in
$>\frac {2\pi }{3}$
in
![]() $\phi (E)$
, which is a contradiction.
$\phi (E)$
, which is a contradiction.
5 Folding
This section is devoted to a technical reduction of Proposition 3.2 to the case where the vertex links of X are not ‘unfoldable’.
By a graph, we mean a (possibly infinite) metric graph with finitely many possible edge lengths. A closed edge-path embedded in a graph
![]() $\Lambda $
is a cycle of
$\Lambda $
is a cycle of
![]() $\Lambda $
. An edge-path I in
$\Lambda $
. An edge-path I in
![]() $\Lambda $
that is embedded, except possibly at the endpoints, is a segment of
$\Lambda $
that is embedded, except possibly at the endpoints, is a segment of
![]() $\Lambda $
if the endpoints of I have degree
$\Lambda $
if the endpoints of I have degree
![]() $\geq 3$
in
$\geq 3$
in
![]() $\Lambda $
, but every internal vertex of I has degree
$\Lambda $
, but every internal vertex of I has degree
![]() $2$
.
$2$
.
Definition 5.1. Let S be a set with an equivalence relation
![]() $\sim $
, each of whose equivalence classes has size
$\sim $
, each of whose equivalence classes has size
![]() $\geq 2$
. A graph is a
$\geq 2$
. A graph is a
![]() $\sim $
-clover if it is obtained from the disjoint union of intervals
$\sim $
-clover if it is obtained from the disjoint union of intervals
![]() $S\times [0,\pi ]$
by identifying all the points in
$S\times [0,\pi ]$
by identifying all the points in
![]() $S\times 0$
to one point called the basepoint and identifying each
$S\times 0$
to one point called the basepoint and identifying each
![]() $s\times \pi $
with
$s\times \pi $
with
![]() $s'\times \pi $
for
$s'\times \pi $
for
![]() $s\sim s'$
. A graph is a clover if it is a
$s\sim s'$
. A graph is a clover if it is a
![]() $\sim $
-clover for some
$\sim $
-clover for some
![]() $S,\sim $
. A graph
$S,\sim $
. A graph
![]() $\Gamma $
is unfoldable at a vertex y if
$\Gamma $
is unfoldable at a vertex y if
![]() $\Gamma $
is a wedge
$\Gamma $
is a wedge
![]() $\Gamma _1\vee \Gamma _2$
at y of a cycle
$\Gamma _1\vee \Gamma _2$
at y of a cycle
![]() $\Gamma _1$
of length
$\Gamma _1$
of length
![]() $2\pi $
and a clover
$2\pi $
and a clover
![]() $\Gamma _2$
with basepoint y (in particular,
$\Gamma _2$
with basepoint y (in particular,
![]() $\Gamma $
is also a clover). See Figure 2.
$\Gamma $
is also a clover). See Figure 2.

Figure 2 An unfoldable graph.
Suppose that we have a triangle complex
![]() $X'$
and a vertex
$X'$
and a vertex
![]() $w'$
contained in distinct edges
$w'$
contained in distinct edges
![]() $e_1=w'v_1, e_2=w'v_2$
of the same length. Suppose that
$e_1=w'v_1, e_2=w'v_2$
of the same length. Suppose that
![]() $\mathrm {lk}^{X'}_{v_1}$
is a circle of length
$\mathrm {lk}^{X'}_{v_1}$
is a circle of length
![]() $2\pi $
and
$2\pi $
and
![]() $\mathrm {lk}^{X'}_{v_2}$
is a clover with basepoint corresponding to
$\mathrm {lk}^{X'}_{v_2}$
is a clover with basepoint corresponding to
![]() $e_2$
. Then the quotient map
$e_2$
. Then the quotient map
![]() $p'\colon X'\to X$
with X obtained from
$p'\colon X'\to X$
with X obtained from
![]() $X'$
by identifying
$X'$
by identifying
![]() $v_1$
with
$v_1$
with
![]() $v_2$
and
$v_2$
and
![]() $e_1$
with
$e_1$
with
![]() $e_2$
is called a folding (note that X might not be a simplicial complex, but in this article, we will be using only the inverse operation to folding which does result in a simplicial complex).
$e_2$
is called a folding (note that X might not be a simplicial complex, but in this article, we will be using only the inverse operation to folding which does result in a simplicial complex).
Conversely, suppose that X is a triangle complex with a vertex v whose link
![]() $\Gamma _1\vee \Gamma _2$
is unfoldable at a point y corresponding to an edge
$\Gamma _1\vee \Gamma _2$
is unfoldable at a point y corresponding to an edge
![]() $vw$
. Then, up to an isometry, there exists a unique triangle complex
$vw$
. Then, up to an isometry, there exists a unique triangle complex
![]() $X'$
and a folding
$X'$
and a folding
![]() $p'\colon X'\to X$
identifying edges
$p'\colon X'\to X$
identifying edges
![]() $w'v_1,w'v_2$
to
$w'v_1,w'v_2$
to
![]() $wv$
and such that the links of
$wv$
and such that the links of
![]() $v_i$
in
$v_i$
in
![]() $X'$
map isometrically to the graphs
$X'$
map isometrically to the graphs
![]() $\Gamma _i$
in the link of v. See Figure 3. We call
$\Gamma _i$
in the link of v. See Figure 3. We call
![]() $p'$
the folding over
$p'$
the folding over
![]() $\Gamma _1$
(since it is uniquely determined by
$\Gamma _1$
(since it is uniquely determined by
![]() $\Gamma _1$
).
$\Gamma _1$
).

Figure 3 A folding
![]() $p'\colon X'\to X$
over
$p'\colon X'\to X$
over
![]() $\Gamma _1$
. Subgraphs corresponding to the links
$\Gamma _1$
. Subgraphs corresponding to the links
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
and their preimages are thickened, the edge
$\Gamma _2$
and their preimages are thickened, the edge
![]() $vw$
and its preimage are dashed.
$vw$
and its preimage are dashed.
Suppose now that
![]() $p'\colon X'\to X,\hat p'\colon \hat X'\to X$
are foldings over
$p'\colon X'\to X,\hat p'\colon \hat X'\to X$
are foldings over
![]() $\Gamma _1\neq \hat \Gamma _1$
. Suppose that
$\Gamma _1\neq \hat \Gamma _1$
. Suppose that
![]() $v\neq \hat w$
and
$v\neq \hat w$
and
![]() $\hat v\neq w$
. We have that
$\hat v\neq w$
. We have that
![]() $\hat \Gamma _1$
lifts to a link
$\hat \Gamma _1$
lifts to a link
![]() $\mathrm {lk}_{v'}^{X'}$
, which is again, unfoldable, except when
$\mathrm {lk}_{v'}^{X'}$
, which is again, unfoldable, except when
![]() $\mathrm {lk}_{v'}^{X'}=\hat \Gamma _1$
. In that exceptional case, we have
$\mathrm {lk}_{v'}^{X'}=\hat \Gamma _1$
. In that exceptional case, we have
![]() $\Gamma _2=\hat \Gamma _1$
and
$\Gamma _2=\hat \Gamma _1$
and
![]() $p'=\hat p'$
, and we set
$p'=\hat p'$
, and we set
![]() $p"=\mathrm {id}$
. Otherwise, let
$p"=\mathrm {id}$
. Otherwise, let
![]() $p"\colon X"\to X'$
be the folding over
$p"\colon X"\to X'$
be the folding over
![]() $\hat \Gamma _1$
. We call
$\hat \Gamma _1$
. We call
![]() $p"\circ p'$
the folding over
$p"\circ p'$
the folding over
![]() $\Gamma _1,\hat \Gamma _1$
. Note that the folding over
$\Gamma _1,\hat \Gamma _1$
. Note that the folding over
![]() $\Gamma _1,\hat \Gamma _1$
coincides with the folding over
$\Gamma _1,\hat \Gamma _1$
coincides with the folding over
![]() $\hat \Gamma _1,\Gamma _1$
.
$\hat \Gamma _1,\Gamma _1$
.
Analogously, given a finite family of foldings
![]() $p^{\prime \lambda }\colon X^{\prime \lambda }\to X$
over
$p^{\prime \lambda }\colon X^{\prime \lambda }\to X$
over
![]() $\Gamma ^{\lambda }_1$
(where
$\Gamma ^{\lambda }_1$
(where
![]() $\lambda $
is an index) with all
$\lambda $
is an index) with all
![]() $v^{\lambda }$
distinct from all
$v^{\lambda }$
distinct from all
![]() $w^{\lambda }$
, the folding over
$w^{\lambda }$
, the folding over
![]() $\{\Gamma ^{\lambda }_1\}$
is the composition of foldings over the lifts of
$\{\Gamma ^{\lambda }_1\}$
is the composition of foldings over the lifts of
![]() $\Gamma ^{\lambda }_1$
, which does not depend on the order. For a countable family of such foldings
$\Gamma ^{\lambda }_1$
, which does not depend on the order. For a countable family of such foldings
![]() $p^{\prime \lambda }\colon X^{\prime \lambda }\to X$
, the folding over
$p^{\prime \lambda }\colon X^{\prime \lambda }\to X$
, the folding over
![]() $\{\Gamma ^{\lambda }_1\}$
is the inverse limit of the foldings over the finite subsets of
$\{\Gamma ^{\lambda }_1\}$
is the inverse limit of the foldings over the finite subsets of
![]() $\{\Gamma ^{\lambda }_1\}$
.
$\{\Gamma ^{\lambda }_1\}$
.
Lemma 5.2. Let
![]() $p_{\mathcal F}\colon X_{\mathcal F}\to X$
be the folding over a (finite or countable) family
$p_{\mathcal F}\colon X_{\mathcal F}\to X$
be the folding over a (finite or countable) family
![]() ${\mathcal F}=\{\Gamma ^{\lambda }_1\}$
.
${\mathcal F}=\{\Gamma ^{\lambda }_1\}$
.
-
(i) The map
 $p_{\mathcal F}$
is a homotopy equivalence.
$p_{\mathcal F}$
is a homotopy equivalence. -
(ii) If X is locally
 $\mathrm {CAT}(0)$
, then
$\mathrm {CAT}(0)$
, then
 $X_{\mathcal F}$
is locally
$X_{\mathcal F}$
is locally
 $\mathrm {CAT}(0)$
.
$\mathrm {CAT}(0)$
. -
(iii) If X is essential, then
 $X_{\mathcal F}$
is essential.
$X_{\mathcal F}$
is essential.
Proof. For part (i), note that if for some indices
![]() $\lambda ,\mu $
, we have
$\lambda ,\mu $
, we have
![]() $v^{\lambda }=v^{\mu }$
, then
$v^{\lambda }=v^{\mu }$
, then
![]() $w^{\lambda }=w^{\mu }$
, since the point
$w^{\lambda }=w^{\mu }$
, since the point
![]() $y^{\lambda }$
in
$y^{\lambda }$
in
![]() $\mathrm {lk}_{v^{\lambda }}^X$
does not depend on
$\mathrm {lk}_{v^{\lambda }}^X$
does not depend on
![]() $\Gamma ^{\lambda }_1$
. Consequently, distinct edges
$\Gamma ^{\lambda }_1$
. Consequently, distinct edges
![]() $v^{\lambda } w^{\lambda }$
might intersect only along
$v^{\lambda } w^{\lambda }$
might intersect only along
![]() $w^{\lambda }$
. Thus, their union
$w^{\lambda }$
. Thus, their union
![]() $V\subset X$
is a forest, and so the quotient map
$V\subset X$
is a forest, and so the quotient map
![]() $q\colon X\to X^*$
collapsing each component of V into a point is a homotopy equivalence. Similarly, the subcomplex
$q\colon X\to X^*$
collapsing each component of V into a point is a homotopy equivalence. Similarly, the subcomplex
![]() $V_{\mathcal F}=p_{\mathcal F}^{-1}(V)\subset X_{\mathcal F}$
is a forest, and so the quotient map
$V_{\mathcal F}=p_{\mathcal F}^{-1}(V)\subset X_{\mathcal F}$
is a forest, and so the quotient map
![]() $q_{\mathcal F}\colon X_{\mathcal F}\to X^*$
collapsing each component of
$q_{\mathcal F}\colon X_{\mathcal F}\to X^*$
collapsing each component of
![]() $V_{\mathcal F} $
into a point is also a homotopy equivalence. Thus, the identity
$V_{\mathcal F} $
into a point is also a homotopy equivalence. Thus, the identity
![]() $q_{\mathcal F} =q\circ p_{\mathcal F}$
implies part (i).
$q_{\mathcal F} =q\circ p_{\mathcal F}$
implies part (i).
Part (ii) follows from the fact that the maps that
![]() $p_{\mathcal F}$
induces between the links of
$p_{\mathcal F}$
induces between the links of
![]() $X_{\mathcal F}$
and X are locally injective and from Theorem E.
$X_{\mathcal F}$
and X are locally injective and from Theorem E.
The map
![]() $p_{\mathcal F}$
is a local isometry at the open edges outside
$p_{\mathcal F}$
is a local isometry at the open edges outside
![]() $V_{\mathcal F}$
. Thus, for part (iii), it suffices to justify that the links of the vertices in each
$V_{\mathcal F}$
. Thus, for part (iii), it suffices to justify that the links of the vertices in each
![]() $p_{\mathcal F}^{-1}(v^{\lambda })$
have no leaves. But each such link is a cycle
$p_{\mathcal F}^{-1}(v^{\lambda })$
have no leaves. But each such link is a cycle
![]() $\Gamma ^{\mu }_1$
(for
$\Gamma ^{\mu }_1$
(for
![]() $v^{\mu }=v^{\lambda }$
) or a clover, as desired.
$v^{\mu }=v^{\lambda }$
) or a clover, as desired.
Proposition 5.3. Let G be a group acting almost freely and without weak inversions on a
![]() $\mathrm {CAT}(0)$
triangle complex X that is an increasing union of connected essential G-c.s. Then G acts almost freely and without weak inversions on a
$\mathrm {CAT}(0)$
triangle complex X that is an increasing union of connected essential G-c.s. Then G acts almost freely and without weak inversions on a
![]() $\mathrm {CAT}(0)$
triangle complex
$\mathrm {CAT}(0)$
triangle complex
![]() $X'$
that is an increasing union of connected essential G-c.s., and none of whose links are unfoldable.
$X'$
that is an increasing union of connected essential G-c.s., and none of whose links are unfoldable.
Furthermore, if X contains an edge of degree
![]() $\geq 3$
, then
$\geq 3$
, then
![]() $X'$
contains an edge of degree
$X'$
contains an edge of degree
![]() $\geq 3$
or G contains a nonabelian free group.
$\geq 3$
or G contains a nonabelian free group.
Proof. We fix an increasing sequence
![]() $Z_k\subset X$
of connected essential G-c.s. exhausting X. A multifolding
$Z_k\subset X$
of connected essential G-c.s. exhausting X. A multifolding
![]() $(X',(Z^{\prime }_k),p')$
is a:
$(X',(Z^{\prime }_k),p')$
is a:
-
(i)
 $\mathrm {CAT}(0)$
triangle complex
$\mathrm {CAT}(0)$
triangle complex
 $X'$
with an action of G,
$X'$
with an action of G, -
(ii) a sequence
 $(Z^{\prime }_k)$
of essential G-c.s. exhausting
$(Z^{\prime }_k)$
of essential G-c.s. exhausting
 $X'$
and
$X'$
and -
(iii) a G-equivariant simplicial map
 $p'\colon X'\to X$
that
$p'\colon X'\to X$
that-
• maps bijectively the set of triangles of each
 $Z^{\prime }_k$
to the set of triangles of
$Z^{\prime }_k$
to the set of triangles of
 $Z_k$
and
$Z_k$
and -
• whose restriction
 $Z^{\prime }_k\to Z_k$
is a homotopy equivalence.
$Z^{\prime }_k\to Z_k$
is a homotopy equivalence.
-
We introduce a partial order
![]() $\leq $
on the set of multifoldings, writing
$\leq $
on the set of multifoldings, writing
![]() $(X',(Z^{\prime }_k),p')\leq (X",(Z^{\prime \prime }_k),p")$
(or, shortly,
$(X',(Z^{\prime }_k),p')\leq (X",(Z^{\prime \prime }_k),p")$
(or, shortly,
![]() $X'\leq X"$
) if there is a G-equivariant simplicial map
$X'\leq X"$
) if there is a G-equivariant simplicial map
![]() $r\colon X"\to X'$
satisfying
$r\colon X"\to X'$
satisfying
![]() $p"=p'\circ r$
. Multifoldings
$p"=p'\circ r$
. Multifoldings
![]() $X',X"$
are equivalent if
$X',X"$
are equivalent if
![]() $X'\leq X"$
and
$X'\leq X"$
and
![]() $X"\leq X'$
. Let
$X"\leq X'$
. Let
![]() $\mathcal X$
be the set of equivalence classes of multifoldings.
$\mathcal X$
be the set of equivalence classes of multifoldings.
We claim that every chain of elements
![]() $X^{\prime \lambda }$
in
$X^{\prime \lambda }$
in
![]() $\mathcal X$
(where
$\mathcal X$
(where
![]() $\lambda $
is an index) has an upper bound. Indeed, denote by
$\lambda $
is an index) has an upper bound. Indeed, denote by
![]() $p^{\prime }_k$
the restriction of
$p^{\prime }_k$
the restriction of
![]() $p'$
to
$p'$
to
![]() $Z^{\prime }_k$
and write
$Z^{\prime }_k$
and write
![]() $(Z^{\prime }_k,p^{\prime }_k)\leq (Z^{\prime \prime }_k,p^{\prime \prime }_k)$
whenever there is a G-equivariant simplicial map
$(Z^{\prime }_k,p^{\prime }_k)\leq (Z^{\prime \prime }_k,p^{\prime \prime }_k)$
whenever there is a G-equivariant simplicial map
![]() $r\colon Z^{\prime \prime }_k\to Z^{\prime }_k$
satisfying
$r\colon Z^{\prime \prime }_k\to Z^{\prime }_k$
satisfying
![]() $p^{\prime \prime }_k=p^{\prime }_k\circ r$
. For each k, since G acts properly and cocompactly on
$p^{\prime \prime }_k=p^{\prime }_k\circ r$
. For each k, since G acts properly and cocompactly on
![]() $Z^{\prime \lambda }_k$
, by the first bullet point, we have that
$Z^{\prime \lambda }_k$
, by the first bullet point, we have that
![]() $(Z^{\prime \lambda }_k, p^{\prime \lambda }_k)$
can take on only finitely values up to the appropriate equivalence. Thus, there exists a largest element among the
$(Z^{\prime \lambda }_k, p^{\prime \lambda }_k)$
can take on only finitely values up to the appropriate equivalence. Thus, there exists a largest element among the
![]() $(Z^{\prime \lambda }_k, p^{\prime \lambda }_k)$
, which we call
$(Z^{\prime \lambda }_k, p^{\prime \lambda }_k)$
, which we call
![]() $Z^{\prime \infty }_k$
. Furthermore, since
$Z^{\prime \infty }_k$
. Furthermore, since
![]() $(Z^{\prime }_{k+1},p^{\prime }_{k+1})\leq (Z^{\prime \prime }_{k+1},p^{\prime \prime }_{k+1})$
implies
$(Z^{\prime }_{k+1},p^{\prime }_{k+1})\leq (Z^{\prime \prime }_{k+1},p^{\prime \prime }_{k+1})$
implies
![]() $(Z^{\prime }_{k},p^{\prime }_k)\leq (Z^{\prime \prime }_{k},p^{\prime \prime }_k)$
, we have natural injective maps
$(Z^{\prime }_{k},p^{\prime }_k)\leq (Z^{\prime \prime }_{k},p^{\prime \prime }_k)$
, we have natural injective maps
![]() $Z^{\prime \infty }_k\to Z^{\prime \infty }_{k+1}$
. Let
$Z^{\prime \infty }_k\to Z^{\prime \infty }_{k+1}$
. Let
![]() $X^{\prime \infty }$
be their direct limit, equipped with the limit map
$X^{\prime \infty }$
be their direct limit, equipped with the limit map
![]() $p^{\prime \infty }$
to X. Since each
$p^{\prime \infty }$
to X. Since each
![]() $Z^{\prime \infty }_k$
is locally
$Z^{\prime \infty }_k$
is locally
![]() $\mathrm {CAT}(0)$
(Corollary 2.3), we have that
$\mathrm {CAT}(0)$
(Corollary 2.3), we have that
![]() $X^{\prime \infty }$
is locally
$X^{\prime \infty }$
is locally
![]() $\mathrm {CAT}(0)$
(Theorem E).
$\mathrm {CAT}(0)$
(Theorem E).
To prove that
![]() $X^{\prime \infty }$
is an upper bound for our chain in
$X^{\prime \infty }$
is an upper bound for our chain in
![]() $\mathcal X$
, by Theorem 2.1, it remains to prove that
$\mathcal X$
, by Theorem 2.1, it remains to prove that
![]() $X^{\prime \infty }$
is simply connected. Let
$X^{\prime \infty }$
is simply connected. Let
![]() $\alpha $
be a closed edge-path in the
$\alpha $
be a closed edge-path in the
![]() $1$
-skeleton of
$1$
-skeleton of
![]() $X^{\prime \infty }$
, and fix k, such that
$X^{\prime \infty }$
, and fix k, such that
![]() $\alpha $
lies in
$\alpha $
lies in
![]() $Z^{\prime \infty }_k$
. Fix
$Z^{\prime \infty }_k$
. Fix
![]() $\lambda $
with
$\lambda $
with
![]() $Z^{\prime \lambda }_k=Z^{\prime \infty }_k$
, and keep the notation
$Z^{\prime \lambda }_k=Z^{\prime \infty }_k$
, and keep the notation
![]() $\alpha $
for its copy in
$\alpha $
for its copy in
![]() $Z^{\prime \lambda }_k$
. Since
$Z^{\prime \lambda }_k$
. Since
![]() $X^{\prime \lambda }$
is simply connected, there is a disc diagram
$X^{\prime \lambda }$
is simply connected, there is a disc diagram
![]() $D\to X^{\prime \lambda }$
with boundary path
$D\to X^{\prime \lambda }$
with boundary path
![]() $\alpha $
. Fix l, such that the image of D is contained in
$\alpha $
. Fix l, such that the image of D is contained in
![]() $Z^{\prime \lambda }_l$
. Since, by the second bullet point, the induced map
$Z^{\prime \lambda }_l$
. Since, by the second bullet point, the induced map
![]() $\pi _1Z^{\prime \infty }_l\to \pi _1Z^{\prime \lambda }_l$
is an isomorphism, we have that
$\pi _1Z^{\prime \infty }_l\to \pi _1Z^{\prime \lambda }_l$
is an isomorphism, we have that
![]() $\alpha $
is trivial in
$\alpha $
is trivial in
![]() $\pi _1Z^{\prime \infty }_l$
and, hence, in
$\pi _1Z^{\prime \infty }_l$
and, hence, in
![]() $\pi _1X^{\prime \infty }$
. Consequently, by the Kuratowski–Zorn lemma, there is a maximal element
$\pi _1X^{\prime \infty }$
. Consequently, by the Kuratowski–Zorn lemma, there is a maximal element
![]() $X'\in \mathcal X$
.
$X'\in \mathcal X$
.
We now prove that none of the links of
![]() $X'$
are unfoldable. Otherwise, suppose that
$X'$
are unfoldable. Otherwise, suppose that
![]() $X'$
has a vertex v whose link
$X'$
has a vertex v whose link
![]() $\Gamma =\Gamma _1\vee \Gamma _2$
is unfoldable at a point corresponding to an edge
$\Gamma =\Gamma _1\vee \Gamma _2$
is unfoldable at a point corresponding to an edge
![]() $vw$
of
$vw$
of
![]() $X'$
. Let
$X'$
. Let
![]() $\mathcal F=\{g\Gamma _1\}$
, for
$\mathcal F=\{g\Gamma _1\}$
, for
![]() $g\in G$
. Since G acts without weak inversions, we have
$g\in G$
. Since G acts without weak inversions, we have
![]() $gv\neq hw$
, for all
$gv\neq hw$
, for all
![]() $g,h\in G$
. Thus, we can define the folding over
$g,h\in G$
. Thus, we can define the folding over
![]() $\mathcal F$
, which we denote by
$\mathcal F$
, which we denote by
![]() $X_{\mathcal F}\to X'$
. The action of G on
$X_{\mathcal F}\to X'$
. The action of G on
![]() $X'$
lifts to an action of G on
$X'$
lifts to an action of G on
![]() $X_{\mathcal F}$
. For each essential G-c.s.
$X_{\mathcal F}$
. For each essential G-c.s.
![]() $Z'\subset X'$
, let
$Z'\subset X'$
, let
![]() $Z_{\mathcal F}\subset X_{\mathcal F}$
be the closure of the union of all the open triangles of
$Z_{\mathcal F}\subset X_{\mathcal F}$
be the closure of the union of all the open triangles of
![]() $X_{\mathcal F}$
mapping into
$X_{\mathcal F}$
mapping into
![]() $Z'$
. Note that if
$Z'$
. Note that if
![]() $Z'$
does not contain v, or if
$Z'$
does not contain v, or if
![]() $Z'$
contains v, but
$Z'$
contains v, but
![]() $\mathrm {lk}^{Z'}_v$
is contained in
$\mathrm {lk}^{Z'}_v$
is contained in
![]() $\Gamma _1$
or
$\Gamma _1$
or
![]() $\Gamma _2$
(in the latter case,
$\Gamma _2$
(in the latter case,
![]() $\mathrm {lk}^{Z'}_v\subset \bigcap _{g\in \mathrm {Stab}(v)}g\Gamma _2$
), then
$\mathrm {lk}^{Z'}_v\subset \bigcap _{g\in \mathrm {Stab}(v)}g\Gamma _2$
), then
![]() $Z_{\mathcal F}\to Z'$
is an isometry. Otherwise,
$Z_{\mathcal F}\to Z'$
is an isometry. Otherwise,
![]() $\mathrm {lk}^{Z'}_v$
contains edges lying on both the cycle
$\mathrm {lk}^{Z'}_v$
contains edges lying on both the cycle
![]() $\Gamma _1$
and the clover
$\Gamma _1$
and the clover
![]() $\Gamma _2$
. Since
$\Gamma _2$
. Since
![]() $Z'$
is essential, the link
$Z'$
is essential, the link
![]() $\mathrm {lk}^{Z'}_v$
is the wedge of
$\mathrm {lk}^{Z'}_v$
is the wedge of
![]() $\Gamma _1$
and a clover, so it is unfoldable. Then
$\Gamma _1$
and a clover, so it is unfoldable. Then
![]() $Z_{\mathcal F}\to Z'$
is the folding over the family
$Z_{\mathcal F}\to Z'$
is the folding over the family
![]() $\{g\Gamma _1\}$
, for
$\{g\Gamma _1\}$
, for
![]() $g\in G$
. By Lemma 5.2(i,iii), we have that
$g\in G$
. By Lemma 5.2(i,iii), we have that
![]() $Z_{\mathcal F}$
is essential and
$Z_{\mathcal F}$
is essential and
![]() $Z_{\mathcal F}\to Z'$
is a homotopy equivalence. By Lemma 5.2(i,ii), we have that
$Z_{\mathcal F}\to Z'$
is a homotopy equivalence. By Lemma 5.2(i,ii), we have that
![]() $X_{\mathcal F}$
is simply connected and locally
$X_{\mathcal F}$
is simply connected and locally
![]() $\mathrm {CAT}(0)$
, and, hence,
$\mathrm {CAT}(0)$
, and, hence,
![]() $\mathrm {CAT}(0)$
by Theorem 2.1. Consequently, we have
$\mathrm {CAT}(0)$
by Theorem 2.1. Consequently, we have
![]() $X_{\mathcal F}\in \mathcal X$
and
$X_{\mathcal F}\in \mathcal X$
and
![]() $X_{\mathcal F}>X'$
, contradicting the maximality of
$X_{\mathcal F}>X'$
, contradicting the maximality of
![]() $X'$
. Thus, none of the links of
$X'$
. Thus, none of the links of
![]() $X'$
are unfoldable.
$X'$
are unfoldable.
For the last assertion, note that, by Lemma 4.1 applied to X, we have that G is neither virtually cyclic, nor virtually
![]() $\mathbb {Z}^2$
. Moreover, G is finitely generated, since it acts properly and cocompactly on
$\mathbb {Z}^2$
. Moreover, G is finitely generated, since it acts properly and cocompactly on
![]() $Z_1$
, which is connected. Consequently, if
$Z_1$
, which is connected. Consequently, if
![]() $X'$
does not have edges of degree
$X'$
does not have edges of degree
![]() $3$
, then by Proposition 3.1, we have that G contains a nonabelian free group, as desired.
$3$
, then by Proposition 3.1, we have that G contains a nonabelian free group, as desired.
6 Criteria for rank 1 elements
In this section, we give criteria for finding ‘rank
![]() $1$
’ elements, and, consequently, free subgroups in G.
$1$
’ elements, and, consequently, free subgroups in G.
Definition 6.1. Let
![]() $\gamma $
be a geodesic line in a
$\gamma $
be a geodesic line in a
![]() $\mathrm {CAT}(0)$
triangle complex X. We say that
$\mathrm {CAT}(0)$
triangle complex X. We say that
![]() $\gamma $
is curved if
$\gamma $
is curved if
![]() $\gamma $
passes through a vertex v and its incoming and outgoing directions at v are at angle
$\gamma $
passes through a vertex v and its incoming and outgoing directions at v are at angle
![]() $>\pi $
.
$>\pi $
.
Lemma 6.2. Let g be a loxodromic isometry of a
![]() $\mathrm {CAT}(0)$
triangle complex X with a curved axis
$\mathrm {CAT}(0)$
triangle complex X with a curved axis
![]() $\gamma $
. Then there exists M, such that the projection to
$\gamma $
. Then there exists M, such that the projection to
![]() $\gamma $
of each closed metric ball in X disjoint from
$\gamma $
of each closed metric ball in X disjoint from
![]() $\gamma $
has diameter
$\gamma $
has diameter
![]() $\leq M$
.
$\leq M$
.
Proof. Suppose that
![]() $\gamma $
passes through a vertex v with incoming and outgoing directions at angle
$\gamma $
passes through a vertex v with incoming and outgoing directions at angle
![]() $>\pi +\kappa ,$
for some
$>\pi +\kappa ,$
for some
![]() $\frac {\pi }{2}>\kappa >0$
. Let R be the translation length of g. We will prove that
$\frac {\pi }{2}>\kappa >0$
. Let R be the translation length of g. We will prove that
![]() $M=R\lceil \frac {2\pi }{\kappa }\rceil $
satisfies the lemma. Otherwise, let
$M=R\lceil \frac {2\pi }{\kappa }\rceil $
satisfies the lemma. Otherwise, let
![]() $x,y$
be points in a closed metric ball disjoint from
$x,y$
be points in a closed metric ball disjoint from
![]() $\gamma $
, such that the projections
$\gamma $
, such that the projections
![]() $x',y'$
of
$x',y'$
of
![]() $x,y$
to
$x,y$
to
![]() $\gamma $
are at distance
$\gamma $
are at distance
![]() $>M$
.
$>M$
.
There are at least
![]() $n=\lceil \frac {2\pi }{\kappa }\rceil $
translates of v under
$n=\lceil \frac {2\pi }{\kappa }\rceil $
translates of v under
![]() $\langle g \rangle $
on
$\langle g \rangle $
on
![]() $x'y'$
distinct from
$x'y'$
distinct from
![]() $x',y'$
. We denote these translates by
$x',y'$
. We denote these translates by
![]() $v^{\prime }_1,\ldots , v^{\prime }_n$
, in the order in which they appear on
$v^{\prime }_1,\ldots , v^{\prime }_n$
, in the order in which they appear on
![]() $x'y'$
. By the continuity of the projection map, there are points
$x'y'$
. By the continuity of the projection map, there are points
![]() $v_1,\ldots ,v_n$
lying on the geodesic
$v_1,\ldots ,v_n$
lying on the geodesic
![]() $xy$
in that order, such that each
$xy$
in that order, such that each
![]() $v_i'$
is the projection of
$v_i'$
is the projection of
![]() $v_i$
to
$v_i$
to
![]() $\gamma $
. We additionally denote
$\gamma $
. We additionally denote
![]() $v_0=x, v_0'=x', v_{n+1}=y,v^{\prime }_{n+1}=y'$
. For
$v_0=x, v_0'=x', v_{n+1}=y,v^{\prime }_{n+1}=y'$
. For
![]() $0\leq i\leq n$
, let
$0\leq i\leq n$
, let
![]() $\beta _i$
denote the geodesic quadrilateral
$\beta _i$
denote the geodesic quadrilateral
![]() $v_iv_{i+1}v^{\prime }_{i+1}v^{\prime }_iv_i$
. The sum of the four Alexandrov angles of each
$v_iv_{i+1}v^{\prime }_{i+1}v^{\prime }_iv_i$
. The sum of the four Alexandrov angles of each
![]() $\beta _i$
is
$\beta _i$
is
![]() $\leq 2\pi $
[Reference Bridson and HaefligerBH99, II.2.11], so the sum of all the Alexandrov angles of all
$\leq 2\pi $
[Reference Bridson and HaefligerBH99, II.2.11], so the sum of all the Alexandrov angles of all
![]() $\beta _i$
is
$\beta _i$
is
![]() $\leq (n+1)2\pi $
.
$\leq (n+1)2\pi $
.
On the other hand, for
![]() $0\leq i<n$
, the sum of the Alexandrov angles of
$0\leq i<n$
, the sum of the Alexandrov angles of
![]() $\beta _i$
and
$\beta _i$
and
![]() $\beta _{i+1}$
at
$\beta _{i+1}$
at
![]() $v_{i+1}$
is
$v_{i+1}$
is
![]() $\geq \pi $
. We will now prove that the sum of the Alexandrov angles of
$\geq \pi $
. We will now prove that the sum of the Alexandrov angles of
![]() $\beta _i$
and
$\beta _i$
and
![]() $\beta _{i+1}$
at
$\beta _{i+1}$
at
![]() $v^{\prime }_{i+1}$
is
$v^{\prime }_{i+1}$
is
![]() $>\pi +\kappa $
. Indeed, if one of them is not equal to the angle in the usual sense (see Section 2), then it equals
$>\pi +\kappa $
. Indeed, if one of them is not equal to the angle in the usual sense (see Section 2), then it equals
![]() $\pi $
. However, since
$\pi $
. However, since
![]() $v^{\prime }_{i+1}$
is the projection of
$v^{\prime }_{i+1}$
is the projection of
![]() $v_{i+1}$
, the second Alexandrov angle is
$v_{i+1}$
, the second Alexandrov angle is
![]() $\geq \frac {\pi }{2}$
, so their sum is
$\geq \frac {\pi }{2}$
, so their sum is
![]() $\geq \frac {3\pi }{2}$
, as desired. Consequently, we have
$\geq \frac {3\pi }{2}$
, as desired. Consequently, we have
![]() $n(\pi +\pi +\kappa )< (n+1)2\pi $
, and so
$n(\pi +\pi +\kappa )< (n+1)2\pi $
, and so
![]() $n\kappa < 2\pi $
, which is a contradiction.
$n\kappa < 2\pi $
, which is a contradiction.
Lemma 6.3. Let G be a group acting almost freely on a
![]() $\mathrm {CAT}(0)$
triangle complex X with a fixed point
$\mathrm {CAT}(0)$
triangle complex X with a fixed point
![]() $\xi $
in the visual boundary of X. Suppose that there is a curved axis
$\xi $
in the visual boundary of X. Suppose that there is a curved axis
![]() $\gamma $
for some
$\gamma $
for some
![]() $g\in G$
with one of the limit points
$g\in G$
with one of the limit points
![]() $\xi $
. Then G is virtually cyclic.
$\xi $
. Then G is virtually cyclic.
Proof. Consider the space of geodesic rays
![]() $\rho \colon [0,\infty )\to X$
representing
$\rho \colon [0,\infty )\to X$
representing
![]() $\xi $
, with the pseudometric
$\xi $
, with the pseudometric
![]() $d(\rho _1,\rho _2)=\inf _{t_1,t_2}d(\rho _1(t_1),\rho _2(t_2))$
. Identifying
$d(\rho _1,\rho _2)=\inf _{t_1,t_2}d(\rho _1(t_1),\rho _2(t_2))$
. Identifying
![]() $\rho _1$
with
$\rho _1$
with
![]() $\rho _2$
for
$\rho _2$
for
![]() $d(\rho _1,\rho _2)=0,$
we obtain a metric space whose metric completion
$d(\rho _1,\rho _2)=0,$
we obtain a metric space whose metric completion
![]() $X_{\xi }$
is
$X_{\xi }$
is
![]() $\mathrm {CAT}(0)$
[Reference LeebLee00, Proposition 2.8]. Since X has geometric dimension
$\mathrm {CAT}(0)$
[Reference LeebLee00, Proposition 2.8]. Since X has geometric dimension
![]() $\leq 2$
(see [Reference KleinerKle99]), by [Reference CapraceCap09, Remark after Corollary 4.4], we have that
$\leq 2$
(see [Reference KleinerKle99]), by [Reference CapraceCap09, Remark after Corollary 4.4], we have that
![]() $X_{\xi }$
has geometric dimension
$X_{\xi }$
has geometric dimension
![]() $\leq 1$
(more precisely, as we learned from Pierre-Emmanuel Caprace, for any
$\leq 1$
(more precisely, as we learned from Pierre-Emmanuel Caprace, for any
![]() $\rho $
representing
$\rho $
representing
![]() $\xi $
, the space
$\xi $
, the space
![]() $X_{\xi }\times \mathbb {R}$
embeds isometrically in the pointed ultralimit of
$X_{\xi }\times \mathbb {R}$
embeds isometrically in the pointed ultralimit of
![]() $(X,\rho (n))_n$
, which has geometric dimension
$(X,\rho (n))_n$
, which has geometric dimension
![]() $\leq 2$
by [Reference LytchakLyt05, Lemma 11.1]). Since G fixes
$\leq 2$
by [Reference LytchakLyt05, Lemma 11.1]). Since G fixes
![]() $\xi $
, the action of G on X induces an action of G on
$\xi $
, the action of G on X induces an action of G on
![]() $X_{\xi }$
.
$X_{\xi }$
.
We will now justify that a complete
![]() $\mathrm {CAT}(0)$
space
$\mathrm {CAT}(0)$
space
![]() $X_{\xi }$
of geometric dimension
$X_{\xi }$
of geometric dimension
![]() $\leq 1$
is an
$\leq 1$
is an
![]() $\mathbb {R}$
-tree, which we learned also from Pierre-Emmanuel Caprace. For a geodesic triangle
$\mathbb {R}$
-tree, which we learned also from Pierre-Emmanuel Caprace. For a geodesic triangle
![]() $xyz$
in
$xyz$
in
![]() $X_{\xi }$
, let
$X_{\xi }$
, let
![]() $x'$
be the projection of x to the geodesic
$x'$
be the projection of x to the geodesic
![]() $yz$
. If
$yz$
. If
![]() $x'\neq x,y$
, then the direction of the geodesic
$x'\neq x,y$
, then the direction of the geodesic
![]() $x'x$
in
$x'x$
in
![]() $\mathrm {lk}_{x'}^{X_{\xi }}$
is distinct from that of the geodesic
$\mathrm {lk}_{x'}^{X_{\xi }}$
is distinct from that of the geodesic
![]() $x'y$
. Thus, the geodesic
$x'y$
. Thus, the geodesic
![]() $xy$
must pass through
$xy$
must pass through
![]() $x'$
, since otherwise mapping it to
$x'$
, since otherwise mapping it to
![]() $\mathrm {lk}_{x'}^{X_{\xi }}$
would give a path between distinct points of a discrete set. Analogously, the geodesic
$\mathrm {lk}_{x'}^{X_{\xi }}$
would give a path between distinct points of a discrete set. Analogously, the geodesic
![]() $xz$
passes through
$xz$
passes through
![]() $x'$
, and so
$x'$
, and so
![]() $xyz$
is
$xyz$
is
![]() $0$
-thin, justifying that
$0$
-thin, justifying that
![]() $X_{\xi }$
is an
$X_{\xi }$
is an
![]() $\mathbb {R}$
-tree.
$\mathbb {R}$
-tree.
Suppose, first, that there is
![]() $h\in G$
acting loxodromically on
$h\in G$
acting loxodromically on
![]() $X_{\xi }$
. Let M be the constant given by Lemma 6.2 for
$X_{\xi }$
. Let M be the constant given by Lemma 6.2 for
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $\rho $
be a ray in
$\rho $
be a ray in
![]() $\gamma $
representing
$\gamma $
representing
![]() $\xi $
. Since h acts loxodromically on
$\xi $
. Since h acts loxodromically on
![]() $X_{\xi }$
, after possibly replacing h by its power, we can assume
$X_{\xi }$
, after possibly replacing h by its power, we can assume
![]() $d(\rho ,h\rho )>M$
. Assume, without loss of generality, that the Busemann function (see [Reference Bridson and HaefligerBH99, II.8.17 and II.8.20]) satisfies
$d(\rho ,h\rho )>M$
. Assume, without loss of generality, that the Busemann function (see [Reference Bridson and HaefligerBH99, II.8.17 and II.8.20]) satisfies
![]() $B_{\xi }(\rho (0))\leq B_{\xi }(h\rho (0))$
. Then for each
$B_{\xi }(\rho (0))\leq B_{\xi }(h\rho (0))$
. Then for each
![]() $t\geq 0$
, the projection
$t\geq 0$
, the projection
![]() $p(t)$
of
$p(t)$
of
![]() $\rho (t)$
to
$\rho (t)$
to
![]() $h\gamma $
is contained in
$h\gamma $
is contained in
![]() $h\rho $
, and for
$h\rho $
, and for
![]() $D=d(\rho (0),h\rho (0))$
, we have
$D=d(\rho (0),h\rho (0))$
, we have
![]() $d(\rho (t),p(t))\leq D$
. Pick
$d(\rho (t),p(t))\leq D$
. Pick
![]() $k\in \mathbb {N}$
with
$k\in \mathbb {N}$
with
![]() $kM>2D$
. Then, by the triangle inequality, we have
$kM>2D$
. Then, by the triangle inequality, we have
![]() $d(p(0),p(2kM))\geq 2kM-2D>kM$
. Consequently, there is
$d(p(0),p(2kM))\geq 2kM-2D>kM$
. Consequently, there is
![]() $0\leq n<k$
, such that
$0\leq n<k$
, such that
![]() $d(p(2nM),p(2(n+1)M))>M$
. Thus, the closed ball of radius M centred at
$d(p(2nM),p(2(n+1)M))>M$
. Thus, the closed ball of radius M centred at
![]() $\rho ((2n+1)M)$
is disjoint from
$\rho ((2n+1)M)$
is disjoint from
![]() $h\gamma $
and contains points
$h\gamma $
and contains points
![]() $\rho (2nM),\rho (2(n+1)M)$
whose projections to
$\rho (2nM),\rho (2(n+1)M)$
whose projections to
![]() $h\gamma $
are at distance
$h\gamma $
are at distance
![]() $>M$
. This contradicts the choice of M.
$>M$
. This contradicts the choice of M.
Consequently, G has a global fixed point in
![]() $X_{\xi }$
(which might not be represented by a geodesic ray but be a point added in the completion). Thus, there is
$X_{\xi }$
(which might not be represented by a geodesic ray but be a point added in the completion). Thus, there is
![]() $D>0$
, such that for any
$D>0$
, such that for any
![]() $\varepsilon>0$
, there is a geodesic ray
$\varepsilon>0$
, there is a geodesic ray
![]() $\rho '$
representing
$\rho '$
representing
![]() $\xi $
at distance
$\xi $
at distance
![]() $\leq D$
from
$\leq D$
from
![]() $\rho $
and satisfying
$\rho $
and satisfying
![]() $d(\rho ',g\rho ')<\varepsilon $
for each
$d(\rho ',g\rho ')<\varepsilon $
for each
![]() $g\in G$
. Consider the homomorphism
$g\in G$
. Consider the homomorphism
![]() $\psi \colon G\to \mathbb {R}$
defined by
$\psi \colon G\to \mathbb {R}$
defined by
![]() $\psi (g)=B_{\xi }(gx)-B_{\xi }(x)$
for any
$\psi (g)=B_{\xi }(gx)-B_{\xi }(x)$
for any
![]() $x\in X$
. We will now justify that
$x\in X$
. We will now justify that
![]() $\psi $
has discrete image. Otherwise, for any
$\psi $
has discrete image. Otherwise, for any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\rho '$
as above, there is
$\rho '$
as above, there is
![]() $t>0$
, such that
$t>0$
, such that
![]() $d(\rho '(t),g\rho '(t))<2\varepsilon $
, but g does not fix a point of X. This contradicts Remark 2.5 applied with Y containing the D-neighbourhood of
$d(\rho '(t),g\rho '(t))<2\varepsilon $
, but g does not fix a point of X. This contradicts Remark 2.5 applied with Y containing the D-neighbourhood of
![]() $\gamma $
.
$\gamma $
.
Let K be the kernel of
![]() $\psi $
. Arguing as in the previous paragraph, we obtain that every
$\psi $
. Arguing as in the previous paragraph, we obtain that every
![]() $g\in K$
fixes a point of X. By [Reference Norin, Osajda and PrzytyckiNOP22, Theorem 1.1(i)], every finitely generated subgroup of K fixes a point of X. Since K acts almost freely, we have that K is finite and so G is virtually cyclic.
$g\in K$
fixes a point of X. By [Reference Norin, Osajda and PrzytyckiNOP22, Theorem 1.1(i)], every finitely generated subgroup of K fixes a point of X. Since K acts almost freely, we have that K is finite and so G is virtually cyclic.
Proposition 6.4. Let G be a group acting almost freely on a
![]() $\mathrm {CAT}(0)$
triangle complex X. Assume that G contains a loxodromic element g with a curved axis
$\mathrm {CAT}(0)$
triangle complex X. Assume that G contains a loxodromic element g with a curved axis
![]() $\gamma $
. Then G is virtually cyclic or contains a nonabelian free group.
$\gamma $
. Then G is virtually cyclic or contains a nonabelian free group.
Proof. By Lemma 6.2, g is rank
![]() $1$
in the sense of [Reference Bestvina and FujiwaraBF09, Definition 5.1]. By Lemma 6.3, we can assume that G does not have a finite index subgroup fixing a limit point of
$1$
in the sense of [Reference Bestvina and FujiwaraBF09, Definition 5.1]. By Lemma 6.3, we can assume that G does not have a finite index subgroup fixing a limit point of
![]() $\gamma $
. Then there is
$\gamma $
. Then there is
![]() $f\in G$
with
$f\in G$
with
![]() $\gamma $
and
$\gamma $
and
![]() $f\gamma $
having disjoint limit point pairs. Consequently, by [Reference Bestvina and FujiwaraBF09, Proposition 5.9], for some n, the elements
$f\gamma $
having disjoint limit point pairs. Consequently, by [Reference Bestvina and FujiwaraBF09, Proposition 5.9], for some n, the elements
![]() $g^n$
and
$g^n$
and
![]() $fg^nf^{-1}$
generate a nonabelian free group.
$fg^nf^{-1}$
generate a nonabelian free group.
7 Extrationality
The main result of this section will be Proposition 7.4, where we will show that in the absence of unfoldable vertices and curved axes, the complex X enjoys a particularly strong rationality property of angles, which we call extrationality.
Definition 7.1. The branching locus E of a triangle complex X is the subcomplex of X that is the union of all the closed edges of degree
![]() $\geq 3$
. A patch of X is a maximal connected subspace P of
$\geq 3$
. A patch of X is a maximal connected subspace P of
![]() $X\setminus E$
, such that
$X\setminus E$
, such that
![]() $P\setminus X^0$
is connected (see Figure 4). If X is simply connected, then by Van Kampen’s theorem, P is a planar surface, and so we can choose an orientation on P.
$P\setminus X^0$
is connected (see Figure 4). If X is simply connected, then by Van Kampen’s theorem, P is a planar surface, and so we can choose an orientation on P.

Figure 4 A patch (in dark grey).
We equip
![]() $P\setminus X^0$
with the length metric induced from
$P\setminus X^0$
with the length metric induced from
![]() $X\setminus X^0$
(see [Reference Bridson and HaefligerBH99, Chapter I.3.24]). Let
$X\setminus X^0$
(see [Reference Bridson and HaefligerBH99, Chapter I.3.24]). Let
![]() $\overline P$
denote the completion of
$\overline P$
denote the completion of
![]() $P\setminus X^0$
, which admits an obvious embedding of P. Furthermore,
$P\setminus X^0$
, which admits an obvious embedding of P. Furthermore,
![]() $\overline P$
admits an obvious triangle complex structure and a simplicial map
$\overline P$
admits an obvious triangle complex structure and a simplicial map
![]() $\overline P\to X$
fitting the following commutative diagram.
$\overline P\to X$
fitting the following commutative diagram.

Note that
![]() $\overline {P}$
is a connected surface with boundary, which we denote
$\overline {P}$
is a connected surface with boundary, which we denote
![]() $\partial P$
.
$\partial P$
.
Definition 7.2. A triangle complex X is piecewise Euclidean if all its triangles are geodesic Euclidean triangles. A piecewise Euclidean triangle complex X is rational if for any vertex v of X, all cycles and segments (see Section 5) in the link of v have lengths commensurable with
![]() $\pi $
. In particular, the angle at v between any edges of the branching locus E is then commensurable with
$\pi $
. In particular, the angle at v between any edges of the branching locus E is then commensurable with
![]() $\pi $
. A rational triangle complex X is extrational if
$\pi $
. A rational triangle complex X is extrational if
-
• for any vertex v of X with a component C of
 $\mathrm {lk}^X_v$
a circle, we have that the length of C is
$\mathrm {lk}^X_v$
a circle, we have that the length of C is
 $2\pi $
and
$2\pi $
and -
• each homomorphism
 $\psi $
defined below is trivial.
$\psi $
defined below is trivial.
We define
![]() $\psi =\psi (P)$
for each patch P of X. Consider the chain complex
$\psi =\psi (P)$
for each patch P of X. Consider the chain complex
![]() $C_*(\overline P,\partial P)$
consisting of those singular chains that are affine with respect to the affine structure on
$C_*(\overline P,\partial P)$
consisting of those singular chains that are affine with respect to the affine structure on
![]() $\overline P$
induced by the piecewise Euclidean metric. Note that the affine structure on
$\overline P$
induced by the piecewise Euclidean metric. Note that the affine structure on
![]() $\overline P$
has singularities at the points x of
$\overline P$
has singularities at the points x of
![]() $\partial P$
with
$\partial P$
with
![]() $\mathrm {lk}_x^{\overline P}$
of length
$\mathrm {lk}_x^{\overline P}$
of length
![]() $\neq \pi $
, and so we require our affine chains to be disjoint from such x except possibly at the vertices. For each
$\neq \pi $
, and so we require our affine chains to be disjoint from such x except possibly at the vertices. For each
![]() $x\in \overline P$
, choose (not necessarily continuously) a direction
$x\in \overline P$
, choose (not necessarily continuously) a direction
![]() $\xi _x\in \mathrm {lk}^{\overline P}_x$
at x, with the only restriction that for
$\xi _x\in \mathrm {lk}^{\overline P}_x$
at x, with the only restriction that for
![]() $x\in \partial P$
, the direction
$x\in \partial P$
, the direction
![]() $\xi _x$
corresponds to one of the edges in
$\xi _x$
corresponds to one of the edges in
![]() $\partial P$
containing x. For an affine singular
$\partial P$
containing x. For an affine singular
![]() $1$
-simplex
$1$
-simplex
![]() $\sigma \to \overline P$
with endpoints x and y, let
$\sigma \to \overline P$
with endpoints x and y, let
![]() $\psi (\sigma )\in \mathbb {R}/\pi \mathbb {Q}$
be the oriented angle between
$\psi (\sigma )\in \mathbb {R}/\pi \mathbb {Q}$
be the oriented angle between
![]() $\xi _x$
and
$\xi _x$
and
![]() $\sigma $
at x minus the oriented angle between
$\sigma $
at x minus the oriented angle between
![]() $\xi _y$
and
$\xi _y$
and
![]() $\sigma $
at y. Note that since X was rational, this equals
$\sigma $
at y. Note that since X was rational, this equals
![]() $0$
mod
$0$
mod
![]() $\pi \mathbb {Q}$
for
$\pi \mathbb {Q}$
for
![]() $\sigma $
in
$\sigma $
in
![]() $\partial P$
, and so we obtain a homomorphism
$\partial P$
, and so we obtain a homomorphism
![]() $\psi \colon C_1(\overline P,\partial P)\to \mathbb {R}/\pi \mathbb {Q}$
. Note that the restriction of
$\psi \colon C_1(\overline P,\partial P)\to \mathbb {R}/\pi \mathbb {Q}$
. Note that the restriction of
![]() $\psi $
to
$\psi $
to
![]() $Z_1(\overline P,\partial P)$
does not depend on the choice of the
$Z_1(\overline P,\partial P)$
does not depend on the choice of the
![]() $\xi _x$
. Furthermore, for each affine singular
$\xi _x$
. Furthermore, for each affine singular
![]() $2$
-simplex
$2$
-simplex
![]() $\tau $
, we have
$\tau $
, we have
![]() $\psi (\partial \tau )=\pm \pi =0$
mod
$\psi (\partial \tau )=\pm \pi =0$
mod
![]() $\pi \mathbb {Q}$
, and so
$\pi \mathbb {Q}$
, and so
![]() $\psi $
descends to a homomorphism
$\psi $
descends to a homomorphism
![]() $\psi \colon H_1(\overline P,\partial P)\to \mathbb {R}/\pi \mathbb {Q}$
. It is not hard to check that our
$\psi \colon H_1(\overline P,\partial P)\to \mathbb {R}/\pi \mathbb {Q}$
. It is not hard to check that our
![]() $H_1(\overline P,\partial P)$
coincides with the usual first (singular) homology group.
$H_1(\overline P,\partial P)$
coincides with the usual first (singular) homology group.
We will need the following variant of [Reference Ballmann and BrinBB95, Lemma 7.4] that was implicit in the proof of [Reference Norin, Osajda and PrzytyckiNOP22, Proposition 3.4].
Lemma 7.3. Let G be a group acting almost freely on a
![]() $\mathrm {CAT}(0)$
triangle complex X that is an increasing union of essential G-c.s. Furthermore, assume that there is a vertex v of X with points
$\mathrm {CAT}(0)$
triangle complex X that is an increasing union of essential G-c.s. Furthermore, assume that there is a vertex v of X with points
![]() $\xi _i,\eta _i\in \mathrm {lk}^X_v$
, for
$\xi _i,\eta _i\in \mathrm {lk}^X_v$
, for
![]() $i=1,\ldots , n,$
such that
$i=1,\ldots , n,$
such that
-
•
 $d^X_v(\xi _i,\eta _i)=\pi $
for
$d^X_v(\xi _i,\eta _i)=\pi $
for
 $i=1,\ldots , n,$
and
$i=1,\ldots , n,$
and -
•
 $d^X_v(\eta _i,\xi _{i+1})\geq \pi $
for
$d^X_v(\eta _i,\xi _{i+1})\geq \pi $
for
 $i=1,\ldots , n-1$
and
$i=1,\ldots , n-1$
and -
•
 $d^X_v(\eta _n, \xi _1)>\pi $
.
$d^X_v(\eta _n, \xi _1)>\pi $
.
Then G contains a loxodromic element g with a curved axis.
Proof. Let
![]() $Z\subset X$
be an essential G-c.s. containing v, such that
$Z\subset X$
be an essential G-c.s. containing v, such that
![]() $\mathrm {lk}^{Z}_v$
contains
$\mathrm {lk}^{Z}_v$
contains
![]() $\xi _i,\eta _i$
, with
$\xi _i,\eta _i$
, with
![]() $d^{Z}_v(\xi _i,\eta _i)=\pi ,$
for
$d^{Z}_v(\xi _i,\eta _i)=\pi ,$
for
![]() $i=1,\ldots , n$
. By [Reference Norin, Osajda and PrzytyckiNOP22, Lemma 5.4] (which was stated in terms of the compact quotient but has the same proof for proper and cocompact actions), for any
$i=1,\ldots , n$
. By [Reference Norin, Osajda and PrzytyckiNOP22, Lemma 5.4] (which was stated in terms of the compact quotient but has the same proof for proper and cocompact actions), for any
![]() $\varepsilon>0$
, there is a path
$\varepsilon>0$
, there is a path
![]() $\omega =\omega _1\cdots \omega _{3n}$
in Z, such that
$\omega =\omega _1\cdots \omega _{3n}$
in Z, such that
-
• paths
 $\omega _j$
are local geodesics in Z, and
$\omega _j$
are local geodesics in Z, and -
• there are
 $g_0=\mathrm {id}, g_1,\ldots , g_n=g\in G$
such that paths
$g_0=\mathrm {id}, g_1,\ldots , g_n=g\in G$
such that paths
 $\omega _{3i+1}$
start at
$\omega _{3i+1}$
start at
 $g_iv$
, paths
$g_iv$
, paths
 $\omega _{3i}$
end at
$\omega _{3i}$
end at
 $g_{i}v$
, and except for that
$g_{i}v$
, and except for that
 $\omega $
is disjoint from the vertex set
$\omega $
is disjoint from the vertex set
 $Z^0$
and transverse to
$Z^0$
and transverse to
 $Z^1$
, and
$Z^1$
, and -
• the starting direction of
 $\omega _{3i+1}$
is at distance
$\omega _{3i+1}$
is at distance
 $<\frac {\varepsilon }{2}$
to
$<\frac {\varepsilon }{2}$
to
 $g_i\xi _{i+1}$
in
$g_i\xi _{i+1}$
in
 $\mathrm {lk}^{Z}_{g_iv}$
, and the ending direction of
$\mathrm {lk}^{Z}_{g_iv}$
, and the ending direction of
 $\omega _{3i}$
is at distance
$\omega _{3i}$
is at distance
 $<\frac {\varepsilon }{2}$
to
$<\frac {\varepsilon }{2}$
to
 $g_i\eta _i$
and
$g_i\eta _i$
and -
• at the remaining breakpoints,
 $\omega _{j}$
and
$\omega _{j}$
and
 $\omega _{j+1}$
are at angle
$\omega _{j+1}$
are at angle
 $>\pi -\varepsilon $
(and
$>\pi -\varepsilon $
(and
 $\leq \pi $
since outside
$\leq \pi $
since outside
 $Z^0$
).
$Z^0$
).
Since
![]() $\omega _j$
are disjoint from
$\omega _j$
are disjoint from
![]() $Z^0$
and transverse to
$Z^0$
and transverse to
![]() $Z^1$
, by Theorem 2.2, they are geodesics in X. The last two bullet points hold in X as well. In particular, at all the breakpoints
$Z^1$
, by Theorem 2.2, they are geodesics in X. The last two bullet points hold in X as well. In particular, at all the breakpoints
![]() $\omega _{j}$
and
$\omega _{j}$
and
![]() $\omega _{j+1}$
are at angle
$\omega _{j+1}$
are at angle
![]() $>\pi -\varepsilon $
. By [Reference Ballmann and BrinBB95, Lemma 2.5], the geodesic
$>\pi -\varepsilon $
. By [Reference Ballmann and BrinBB95, Lemma 2.5], the geodesic
![]() $\gamma $
in X with the same endpoints as
$\gamma $
in X with the same endpoints as
![]() $\omega $
starts and ends in directions at distance
$\omega $
starts and ends in directions at distance
![]() $<(3n-1)\varepsilon $
to
$<(3n-1)\varepsilon $
to
![]() $\xi _1,g\eta _n$
. Consequently, for
$\xi _1,g\eta _n$
. Consequently, for
![]() $\varepsilon $
sufficiently small, by Theorem 2.2, we have that
$\varepsilon $
sufficiently small, by Theorem 2.2, we have that
![]() $\bigcup _{l\in \mathbb {Z}}g^l\gamma $
is a curved axis for g.
$\bigcup _{l\in \mathbb {Z}}g^l\gamma $
is a curved axis for g.
Proposition 7.4. Let G be a group acting almost freely on a
![]() $\mathrm {CAT}(0)$
triangle complex X that is an increasing union of essential G-c.s. and none of whose links are unfoldable. If X is not G-equivariantly isometric (by a possibly nonsimplicial isometry) to a piecewise Euclidean triangle complex
$\mathrm {CAT}(0)$
triangle complex X that is an increasing union of essential G-c.s. and none of whose links are unfoldable. If X is not G-equivariantly isometric (by a possibly nonsimplicial isometry) to a piecewise Euclidean triangle complex
![]() $X'$
or X is isometric to such
$X'$
or X is isometric to such
![]() $X'$
but
$X'$
but
![]() $X'$
is not extrational, then G is virtually cyclic or contains a nonabelian free group.
$X'$
is not extrational, then G is virtually cyclic or contains a nonabelian free group.
Proof. To prove that G is virtually cyclic or contains a nonabelian free group in each case we will show the existence of a curved axis in X (or in a different
![]() $\mathrm {CAT}(0)$
triangle complex
$\mathrm {CAT}(0)$
triangle complex
![]() $\overline X$
) for an element of G, since then the proposition follows from Proposition 6.4.
$\overline X$
) for an element of G, since then the proposition follows from Proposition 6.4.
Assume first that X is not G-equivariantly isometric to a piecewise Euclidean triangle complex
![]() $X'$
. Then by [Reference Ballmann and BrinBB95, Proposition 2.11] there is
$X'$
. Then by [Reference Ballmann and BrinBB95, Proposition 2.11] there is
-
(i) a point in the interior of a triangle of X with negative Gaussian curvature, or
-
(ii) a point in the interior of an edge of X with negative sum of geodesic curvatures of some two incident triangles, or
-
(iii) a vertex v of X with
 $\mathrm {lk}^X_v$
a circle of length
$\mathrm {lk}^X_v$
a circle of length
 $>2\pi $
.
$>2\pi $
.
In case (iii), or, more generally, if
![]() $\mathrm {lk}^X_v$
has a component C that is a circle of length
$\mathrm {lk}^X_v$
has a component C that is a circle of length
![]() $>2\pi $
, let
$>2\pi $
, let
![]() $\xi _1,\eta _1$
be points at distance
$\xi _1,\eta _1$
be points at distance
![]() $\pi $
in C, and let
$\pi $
in C, and let
![]() $\eta _2,\xi _2$
be their antipodal points. Applying Lemma 7.3 with
$\eta _2,\xi _2$
be their antipodal points. Applying Lemma 7.3 with
![]() $n=2$
, we obtain a curved axis. In cases (i) and (ii), by [Reference Norin, Osajda and PrzytyckiNOP22, Lemma 5.5], there is a
$n=2$
, we obtain a curved axis. In cases (i) and (ii), by [Reference Norin, Osajda and PrzytyckiNOP22, Lemma 5.5], there is a
![]() $\mathrm {CAT}(0)$
triangle complex
$\mathrm {CAT}(0)$
triangle complex
![]() $\overline X$
, obtained from X by a G-equivariant subdivision and a G-equivariant replacement of the smooth Riemannian metrics, with a vertex
$\overline X$
, obtained from X by a G-equivariant subdivision and a G-equivariant replacement of the smooth Riemannian metrics, with a vertex
![]() $u\in \overline X$
whose
$u\in \overline X$
whose
![]() $\mathrm {lk}^{\overline X}_u$
is either
$\mathrm {lk}^{\overline X}_u$
is either
-
• a circle of length
 $>2\pi $
or
$>2\pi $
or -
• a graph obtained from a family of disjoint circles
 $C_1,C_2,\ldots $
of length
$C_1,C_2,\ldots $
of length
 $2\pi $
by glueing them along a nontrivial arc b of length
$2\pi $
by glueing them along a nontrivial arc b of length
 $<\pi $
.
$<\pi $
.
The first bullet point brings us to case (iii). In the case of the second bullet point, let
![]() $\xi _1,\xi _2\in C_1\setminus b$
and
$\xi _1,\xi _2\in C_1\setminus b$
and
![]() $\eta _1,\eta _2\in C_2\setminus b$
be points at distance
$\eta _1,\eta _2\in C_2\setminus b$
be points at distance
![]() $\frac {\pi }{2}$
from the endpoints of b, with
$\frac {\pi }{2}$
from the endpoints of b, with
![]() $d^{\overline X}_u(\xi _1,\eta _1)=d^{\overline X}_u(\xi _2,\eta _2)=\pi $
. Applying Lemma 7.3 with
$d^{\overline X}_u(\xi _1,\eta _1)=d^{\overline X}_u(\xi _2,\eta _2)=\pi $
. Applying Lemma 7.3 with
![]() $n=2$
, we obtain a curved axis in
$n=2$
, we obtain a curved axis in
![]() $\overline X$
, as desired.
$\overline X$
, as desired.
Thus, without loss of generality, we can assume that X is a piecewise Euclidean triangle complex. If X is not rational, then by [Reference Ballmann and BrinBB95, Proposition 7.7], applied to an essential G-c.s., there is a closed locally injective edge-path
![]() $\beta $
in some
$\beta $
in some
![]() $\mathrm {lk}^X_v$
whose length is not commensurable with
$\mathrm {lk}^X_v$
whose length is not commensurable with
![]() $\pi $
. In particular, by [Reference Ballmann and BrinBB95, Lemma 6.1(iii)], there are points
$\pi $
. In particular, by [Reference Ballmann and BrinBB95, Lemma 6.1(iii)], there are points
![]() $\xi ,\eta $
in
$\xi ,\eta $
in
![]() $\mathrm {lk}^X_v$
at distance
$\mathrm {lk}^X_v$
at distance
![]() $>\pi +\delta ,$
for some
$>\pi +\delta ,$
for some
![]() $\delta>0$
(one could apply [Reference Norin, Osajda and PrzytyckiNOP22, Corollary 1.7] to find such
$\delta>0$
(one could apply [Reference Norin, Osajda and PrzytyckiNOP22, Corollary 1.7] to find such
![]() $\xi ,\eta $
in
$\xi ,\eta $
in
![]() $\beta $
, but it does not simplify the argument). Let
$\beta $
, but it does not simplify the argument). Let
![]() $\beta _-$
(respectively,
$\beta _-$
(respectively,
![]() $\beta _+$
) be the shortest path from
$\beta _+$
) be the shortest path from
![]() $\xi $
(respectively,
$\xi $
(respectively,
![]() $\eta $
) to
$\eta $
) to
![]() $\beta $
. Since the length of
$\beta $
. Since the length of
![]() $\beta $
is not commensurable with
$\beta $
is not commensurable with
![]() $\pi $
, there is a path
$\pi $
, there is a path
![]() $\beta _-\beta _0\beta _+$
with
$\beta _-\beta _0\beta _+$
with
![]() $\beta _0$
factoring through the universal cover of
$\beta _0$
factoring through the universal cover of
![]() $\beta $
whose length equals
$\beta $
whose length equals
![]() $(2n-1)\pi +\delta '$
for some
$(2n-1)\pi +\delta '$
for some
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $0\leq \delta '\leq \delta $
. Choosing
$0\leq \delta '\leq \delta $
. Choosing
![]() $\xi _1=\xi ,\eta _1,\xi _2,\ldots , \eta _{n}$
as consecutive points at distance
$\xi _1=\xi ,\eta _1,\xi _2,\ldots , \eta _{n}$
as consecutive points at distance
![]() $\pi $
along that path, we have
$\pi $
along that path, we have
![]() $d^{X}_v(\xi _1,\eta _n)>\pi $
. Applying Lemma 7.3, we obtain a curved axis.
$d^{X}_v(\xi _1,\eta _n)>\pi $
. Applying Lemma 7.3, we obtain a curved axis.
Finally, if X is not extrational, let P be a patch of X with nontrivial
![]() $\psi =\psi (P)$
. Since P is planar, there is an element in
$\psi =\psi (P)$
. Since P is planar, there is an element in
![]() $H_1(\overline P,\partial P)$
represented by a piecewise affine path
$H_1(\overline P,\partial P)$
represented by a piecewise affine path
![]() $\alpha $
in
$\alpha $
in
![]() $\overline P$
with endpoints in
$\overline P$
with endpoints in
![]() $\partial P$
and
$\partial P$
and
![]() $\psi (\alpha )\neq 0$
. Let
$\psi (\alpha )\neq 0$
. Let
![]() $\alpha $
be shortest among such paths, which exists since
$\alpha $
be shortest among such paths, which exists since
![]() $\mathrm {Stab}(P)$
acts cocompactly on
$\mathrm {Stab}(P)$
acts cocompactly on
![]() $\overline P$
. Note that then
$\overline P$
. Note that then
![]() $\alpha $
does not intersect
$\alpha $
does not intersect
![]() $\partial P$
except at its endpoints, since, otherwise, we could decompose it into two shorter paths, with
$\partial P$
except at its endpoints, since, otherwise, we could decompose it into two shorter paths, with
![]() $\psi $
nontrivial on at least one of them. Thus, the image of
$\psi $
nontrivial on at least one of them. Thus, the image of
![]() $\alpha $
in X (for which we keep the same notation) is a local geodesic in X that intersects the branching locus E exactly at its endpoints
$\alpha $
in X (for which we keep the same notation) is a local geodesic in X that intersects the branching locus E exactly at its endpoints
![]() $x,x'$
. Let e (respectively,
$x,x'$
. Let e (respectively,
![]() $e'$
) be the segment of
$e'$
) be the segment of
![]() $\mathrm {lk}^X_x$
(respectively,
$\mathrm {lk}^X_x$
(respectively,
![]() $\mathrm {lk}^X_{x'}$
) containing the point corresponding to the direction of
$\mathrm {lk}^X_{x'}$
) containing the point corresponding to the direction of
![]() $\alpha $
. By the shortness condition, we have that e (respectively,
$\alpha $
. By the shortness condition, we have that e (respectively,
![]() $e'$
) has endpoints at distance
$e'$
) has endpoints at distance
![]() $\geq \frac {\pi }{2}$
from x (respectively,
$\geq \frac {\pi }{2}$
from x (respectively,
![]() $x'$
), and so is of length
$x'$
), and so is of length
![]() $\geq \pi $
. They cannot both have length
$\geq \pi $
. They cannot both have length
![]() $\pi $
, since then we would have
$\pi $
, since then we would have
![]() $\psi (\alpha )=0$
, so assume, without loss of generality, that the length l of e is
$\psi (\alpha )=0$
, so assume, without loss of generality, that the length l of e is
![]() $>\pi $
.
$>\pi $
.
If
![]() $l> 2\pi $
, then it is easy to find points
$l> 2\pi $
, then it is easy to find points
![]() $\eta _1,\xi _1,\xi _2,\eta _2$
lying on l in that order and satisfying the hypothesis of Lemma 7.3 with
$\eta _1,\xi _1,\xi _2,\eta _2$
lying on l in that order and satisfying the hypothesis of Lemma 7.3 with
![]() $n=2$
. If
$n=2$
. If
![]() $2\pi> l>\pi $
or
$2\pi> l>\pi $
or
![]() $l=2\pi $
and the endpoints of e are distinct, then the construction of such points is given in the proof of [Reference Ballmann and BrinBB95, Lemma 7.6]. It remains to consider the case where
$l=2\pi $
and the endpoints of e are distinct, then the construction of such points is given in the proof of [Reference Ballmann and BrinBB95, Lemma 7.6]. It remains to consider the case where
![]() $l=2\pi $
and where both endpoints of e are equal to a vertex y. Let
$l=2\pi $
and where both endpoints of e are equal to a vertex y. Let
![]() $\Gamma _2$
be the graph obtained from
$\Gamma _2$
be the graph obtained from
![]() $\mathrm {lk}^X_x$
by removing e. If
$\mathrm {lk}^X_x$
by removing e. If
![]() $\Gamma _2$
contains a point z at distance
$\Gamma _2$
contains a point z at distance
![]() $>\pi $
from y, then it is easy to find points
$>\pi $
from y, then it is easy to find points
![]() $\xi _1,\eta _1,\xi _2,\eta _2$
on a geodesic from z to the midpoint of e satisfying the hypothesis of Lemma 7.3 with
$\xi _1,\eta _1,\xi _2,\eta _2$
on a geodesic from z to the midpoint of e satisfying the hypothesis of Lemma 7.3 with
![]() $n=2$
. Otherwise,
$n=2$
. Otherwise,
![]() $\Gamma _2$
is a clover, contradicting the assumption that
$\Gamma _2$
is a clover, contradicting the assumption that
![]() $\mathrm {lk}^X_x$
is not unfoldable.
$\mathrm {lk}^X_x$
is not unfoldable.
8 Sheared geodesics
In this section, we prove that the following piecewise geodesics have distinct endpoints. We will use some vocabulary from Section 4.
Definition 8.1. A sheared geodesic in a piecewise Euclidean triangle complex X is a concatenation
![]() $\gamma _1\cdot \gamma _2\cdots \gamma _{2k-1}\cdot \gamma _{2k}$
of geodesics, such that (see Figure 5):
$\gamma _1\cdot \gamma _2\cdots \gamma _{2k-1}\cdot \gamma _{2k}$
of geodesics, such that (see Figure 5):
-
• for
 $i=1,\ldots , k,$
the (possibly trivial) geodesic
$i=1,\ldots , k,$
the (possibly trivial) geodesic
 $\gamma _{2i}$
lies in the interior of an edge
$\gamma _{2i}$
lies in the interior of an edge
 $e_i$
of X and
$e_i$
of X and -
• for
 $i=1,\ldots , k-1,$
the geodesic
$i=1,\ldots , k-1,$
the geodesic
 $\gamma _{2i-1}$
ends and the geodesic
$\gamma _{2i-1}$
ends and the geodesic
 $\gamma _{2i+1}$
starts perpendicularly to
$\gamma _{2i+1}$
starts perpendicularly to
 $e_i$
in triangles of X that are distinct, and the geodesic
$e_i$
in triangles of X that are distinct, and the geodesic
 $\gamma _{2k-1}$
ends perpendicularly to
$\gamma _{2k-1}$
ends perpendicularly to
 $e_k$
in a triangle.
$e_k$
in a triangle.

Figure 5 A sheared geodesic.
Proposition 8.2. Let X be a piecewise Euclidean triangle complex that is
![]() $\mathrm {CAT}(0)$
. Let
$\mathrm {CAT}(0)$
. Let
![]() $\gamma $
in X be a sheared geodesic. Then
$\gamma $
in X be a sheared geodesic. Then
![]() $\gamma $
is not a closed path.
$\gamma $
is not a closed path.
The proof will use the following two building blocks.
Lemma 8.3. Let X be a piecewise Euclidean triangle complex that is
![]() $\mathrm {CAT}(0)$
. Let
$\mathrm {CAT}(0)$
. Let
![]() $xy$
be a nontrivial geodesic in X, such that y belongs to the interior of an edge e of X and
$xy$
be a nontrivial geodesic in X, such that y belongs to the interior of an edge e of X and
![]() $xy$
ends in a triangle T. Then for any z in the interior of e, the geodesic
$xy$
ends in a triangle T. Then for any z in the interior of e, the geodesic
![]() $xz$
is nontrivial and ends in T.
$xz$
is nontrivial and ends in T.
Proof. We have
![]() $z\neq x$
since edges are geodesics, and so, in particular, x does not lie in e. If for some z in the interior of e the geodesic
$z\neq x$
since edges are geodesics, and so, in particular, x does not lie in e. If for some z in the interior of e the geodesic
![]() $xz$
does not end in T, then, since the geodesic
$xz$
does not end in T, then, since the geodesic
![]() $xz$
varies continuously with z, for some z in the interior of e, the geodesic
$xz$
varies continuously with z, for some z in the interior of e, the geodesic
![]() $xz$
ends in e. Denote by
$xz$
ends in e. Denote by
![]() $e_1, e_2$
the two subedges into which such z divides e. Suppose that
$e_1, e_2$
the two subedges into which such z divides e. Suppose that
![]() $xz$
ends in
$xz$
ends in
![]() $e_1$
. Then the entire
$e_1$
. Then the entire
![]() $e_1$
must lie in
$e_1$
must lie in
![]() $xz$
. Moreover, appending
$xz$
. Moreover, appending
![]() $xz$
by
$xz$
by
![]() $e_2$
, we also obtain a geodesic (Theorem 2.2). Since y lies in
$e_2$
, we also obtain a geodesic (Theorem 2.2). Since y lies in
![]() $e=e_1\cdot e_2$
, this shows that
$e=e_1\cdot e_2$
, this shows that
![]() $xy$
ends in e, which is a contradiction.
$xy$
ends in e, which is a contradiction.
Lemma 8.4. Let X be a piecewise Euclidean triangle complex that is
![]() $\mathrm {CAT}(0)$
. Let
$\mathrm {CAT}(0)$
. Let
![]() $xz$
be a nontrivial geodesic in X, such that z belongs to the interior of an edge e of X and
$xz$
be a nontrivial geodesic in X, such that z belongs to the interior of an edge e of X and
![]() $xz$
ends in a triangle T. Suppose that y belongs to the interior of an edge
$xz$
ends in a triangle T. Suppose that y belongs to the interior of an edge
![]() $e'$
of X and
$e'$
of X and
![]() $zy$
is a nontrivial geodesic in X that starts perpendicularly to e in a triangle distinct from T and ends perpendicularly to
$zy$
is a nontrivial geodesic in X that starts perpendicularly to e in a triangle distinct from T and ends perpendicularly to
![]() $e'$
in a triangle
$e'$
in a triangle
![]() $T'$
. Then the geodesic
$T'$
. Then the geodesic
![]() $xy$
is nontrivial and ends in
$xy$
is nontrivial and ends in
![]() $T'$
.
$T'$
.
Proof. Consider the geodesic triangle
![]() $xyz$
. By our assumptions, its Alexandrov angle at z is
$xyz$
. By our assumptions, its Alexandrov angle at z is
![]() $>\frac {\pi }{2}$
, and so, in particular,
$>\frac {\pi }{2}$
, and so, in particular,
![]() $x\neq y$
, and its Alexandrov angle at y is
$x\neq y$
, and its Alexandrov angle at y is
![]() $<\frac {\pi }{2}$
. Since
$<\frac {\pi }{2}$
. Since
![]() $zy$
ends in a triangle
$zy$
ends in a triangle
![]() $T'$
perpendicularly to
$T'$
perpendicularly to
![]() $e'$
, we have that
$e'$
, we have that
![]() $xy$
ends in
$xy$
ends in
![]() $T'$
, as desired.
$T'$
, as desired.
Proof of Proposition 8.2
Let
![]() $\gamma =\gamma _1\cdot \gamma _2\cdots \gamma _{2k-1}\cdot \gamma _{2k}$
as in Definition 8.1. For
$\gamma =\gamma _1\cdot \gamma _2\cdots \gamma _{2k-1}\cdot \gamma _{2k}$
as in Definition 8.1. For
![]() $i=1,\ldots , k,$
denote
$i=1,\ldots , k,$
denote
![]() $\gamma _{2i}=y_iz_i$
and denote by
$\gamma _{2i}=y_iz_i$
and denote by
![]() $T_i$
the triangle in which
$T_i$
the triangle in which
![]() $\gamma _{2i-1}$
ends. Let x be the starting point of
$\gamma _{2i-1}$
ends. Let x be the starting point of
![]() $\gamma _{1}$
. We prove by induction on
$\gamma _{1}$
. We prove by induction on
![]() $i=1,\ldots , k,$
that x and
$i=1,\ldots , k,$
that x and
![]() $z_i$
are distinct and that the geodesic
$z_i$
are distinct and that the geodesic
![]() $xz_i$
ends in
$xz_i$
ends in
![]() $T_i$
. The proposition follows from this induction hypothesis applied with
$T_i$
. The proposition follows from this induction hypothesis applied with
![]() $i=k$
.
$i=k$
.
For
![]() $i=1$
, the induction hypothesis follows from Lemma 8.3. Suppose now that we have established it for some
$i=1$
, the induction hypothesis follows from Lemma 8.3. Suppose now that we have established it for some
![]() $i=m<k$
. Then, by Lemma 8.4, the geodesic
$i=m<k$
. Then, by Lemma 8.4, the geodesic
![]() $xy_{m+1}$
is nontrivial and ends in
$xy_{m+1}$
is nontrivial and ends in
![]() $T_{m+1}$
. Thus, by Lemma 8.3, the induction hypothesis holds for
$T_{m+1}$
. Thus, by Lemma 8.3, the induction hypothesis holds for
![]() $i=m+1$
.
$i=m+1$
.
9 Free
Proof of Proposition 3.2
By Proposition 5.3, we can assume that none of the vertex links of X are unfoldable. Thus, by Proposition 7.4 and Lemma 4.1(i), we can assume that X is piecewise Euclidean and extrational. Let
![]() $Z\subset X$
be a thick G-c.s. Note that each patch of X either has no triangle in Z or is contained in Z, in which case, we call it a Z-patch.
$Z\subset X$
be a thick G-c.s. Note that each patch of X either has no triangle in Z or is contained in Z, in which case, we call it a Z-patch.
Since X is rational, and Z is a G-c.s., there is
![]() $q\in \mathbb {N}$
, such that for each Z-patch P and each vertex
$q\in \mathbb {N}$
, such that for each Z-patch P and each vertex
![]() $v\in \partial P$
, the length of
$v\in \partial P$
, the length of
![]() $\mathrm {lk}_v^{\overline P}$
is a multiplicity of
$\mathrm {lk}_v^{\overline P}$
is a multiplicity of
![]() $\frac {\pi }{q}$
. For each Z-patch P, we define the homomorphism
$\frac {\pi }{q}$
. For each Z-patch P, we define the homomorphism
![]() $\psi '=\psi '(P)\colon H_1(\overline P,\partial P)\to \mathbb {R}/\frac {\pi }{q}\mathbb {Z}$
in the same way as
$\psi '=\psi '(P)\colon H_1(\overline P,\partial P)\to \mathbb {R}/\frac {\pi }{q}\mathbb {Z}$
in the same way as
![]() $\psi $
, but replacing
$\psi $
, but replacing
![]() $\pi \mathbb {Q}$
by
$\pi \mathbb {Q}$
by
![]() $\frac {\pi }{q}\mathbb {Z}$
. We have
$\frac {\pi }{q}\mathbb {Z}$
. We have
![]() $\psi =\psi '$
mod
$\psi =\psi '$
mod
![]() $\pi \mathbb {Q}$
. Since
$\pi \mathbb {Q}$
. Since
![]() $\psi $
is trivial, the image of
$\psi $
is trivial, the image of
![]() $\psi '$
is contained in
$\psi '$
is contained in
![]() $\pi \mathbb {Q}/\frac {\pi }{q}\mathbb {Z}$
. Since there are finitely many G-orbits of Z-patches, and since each
$\pi \mathbb {Q}/\frac {\pi }{q}\mathbb {Z}$
. Since there are finitely many G-orbits of Z-patches, and since each
![]() $H_1(\overline P,\partial P)$
is finitely generated as a
$H_1(\overline P,\partial P)$
is finitely generated as a
![]() $\mathrm {Stab}(P)$
-module, there is
$\mathrm {Stab}(P)$
-module, there is
![]() $q'\in \mathbb {N}$
, such that the image of each
$q'\in \mathbb {N}$
, such that the image of each
![]() $\psi '$
is contained in
$\psi '$
is contained in
![]() $\frac {\pi }{q'}\mathbb {Z}/\frac {\pi }{q}\mathbb {Z}$
. Consequently, for any Z-patch P, any geodesic
$\frac {\pi }{q'}\mathbb {Z}/\frac {\pi }{q}\mathbb {Z}$
. Consequently, for any Z-patch P, any geodesic
![]() $xy$
in
$xy$
in
![]() $\overline P$
disjoint from
$\overline P$
disjoint from
![]() $\partial P$
, except at its endpoints, that is at angle
$\partial P$
, except at its endpoints, that is at angle
![]() $\in \frac {\pi }{q'}\mathbb {Z}$
from
$\in \frac {\pi }{q'}\mathbb {Z}$
from
![]() $\partial P$
at x, is also at angle
$\partial P$
at x, is also at angle
![]() $\in \frac {\pi }{q'}\mathbb {Z}$
from
$\in \frac {\pi }{q'}\mathbb {Z}$
from
![]() $\partial P$
at y. Without loss of generality, assume that
$\partial P$
at y. Without loss of generality, assume that
![]() $q'$
is even.
$q'$
is even.
We need the following variant of the Liouville measure
![]() $\mu $
from [Reference Ballmann and BrinBB95, Section 3]. Let S be the set of all the directions
$\mu $
from [Reference Ballmann and BrinBB95, Section 3]. Let S be the set of all the directions
![]() $\xi $
at an angle
$\xi $
at an angle
![]() $\theta (\xi )\in \frac {\pi }{q'}\mathbb {Z}\cap (-\frac {\pi }{2},\frac {\pi }{2})$
from a direction normal to E in the links
$\theta (\xi )\in \frac {\pi }{q'}\mathbb {Z}\cap (-\frac {\pi }{2},\frac {\pi }{2})$
from a direction normal to E in the links
![]() $\mathrm {lk}_x^Z$
for all the points
$\mathrm {lk}_x^Z$
for all the points
![]() $x\in Z$
that lie in the interior of an edge e of E. The Liouville measure
$x\in Z$
that lie in the interior of an edge e of E. The Liouville measure
![]() $d\mu (\xi )$
on S is given as
$d\mu (\xi )$
on S is given as
![]() $\cos \theta (\xi )dx$
, where
$\cos \theta (\xi )dx$
, where
![]() $dx$
is the volume element on e. Let
$dx$
is the volume element on e. Let
![]() $V\subset S$
be the full measure subset of S of directions
$V\subset S$
be the full measure subset of S of directions
![]() $\xi $
, such that each geodesic ray
$\xi $
, such that each geodesic ray
![]() $\gamma $
in Z with starting direction
$\gamma $
in Z with starting direction
![]() $\xi $
is disjoint from
$\xi $
is disjoint from
![]() $Z^0$
. Let
$Z^0$
. Let
![]() $F\colon V\to \mathcal P(V)$
be the map defined by
$F\colon V\to \mathcal P(V)$
be the map defined by
![]() $\eta \in F(\xi )$
for
$\eta \in F(\xi )$
for
![]() $\eta \in \mathrm {lk}_x^Z$
if there exists a geodesic
$\eta \in \mathrm {lk}_x^Z$
if there exists a geodesic
![]() $yz$
in Z with starting direction
$yz$
in Z with starting direction
![]() $\xi $
, intersecting E only in y and x and with
$\xi $
, intersecting E only in y and x and with
![]() $\eta $
being the direction at x of
$\eta $
being the direction at x of
![]() $xz$
. Since G acts on Z properly and cocompactly, we have that each
$xz$
. Since G acts on Z properly and cocompactly, we have that each
![]() $F(\xi )$
is finite. We can thus define a Markov chain with states V and transition probabilities
$F(\xi )$
is finite. We can thus define a Markov chain with states V and transition probabilities
![]() $\frac {1}{|F(\xi )|}$
from
$\frac {1}{|F(\xi )|}$
from
![]() $\xi $
to each
$\xi $
to each
![]() $\eta \in F(\xi )$
. By (the calculation in) [Reference Ballmann and BrinBB95, Proposition 3.3], the measure
$\eta \in F(\xi )$
. By (the calculation in) [Reference Ballmann and BrinBB95, Proposition 3.3], the measure
![]() $\mu $
is stationary for this Markov chain. Thus, the space
$\mu $
is stationary for this Markov chain. Thus, the space
![]() $V^{\mathbb {Z}}$
can be equipped with Markov measure
$V^{\mathbb {Z}}$
can be equipped with Markov measure
![]() $\mu ^*$
invariant under the shift (see, e.g. [Reference WaltersWal82, Example (8), page 21]). Since Z is a G-c.s., the quotient
$\mu ^*$
invariant under the shift (see, e.g. [Reference WaltersWal82, Example (8), page 21]). Since Z is a G-c.s., the quotient
![]() $V^{\mathbb {Z}}/G$
by the diagonal action of G is of finite measure. Note that the shift map descends to
$V^{\mathbb {Z}}/G$
by the diagonal action of G is of finite measure. Note that the shift map descends to
![]() $V^{\mathbb {Z}}/G$
and is still measure preserving.
$V^{\mathbb {Z}}/G$
and is still measure preserving.
Let e be an edge of Z lying in three distinct triangles
![]() $T_a,T_b,T_c$
of Z. Let
$T_a,T_b,T_c$
of Z. Let
![]() $V^{ab}\subset V^{\mathbb {Z}}$
be the set of
$V^{ab}\subset V^{\mathbb {Z}}$
be the set of
![]() $(\xi _i)_i$
, such that
$(\xi _i)_i$
, such that
-
• we have
 $\xi _1\in \mathrm {lk}_x^{T_a}$
for
$\xi _1\in \mathrm {lk}_x^{T_a}$
for
 $x\in e$
, and
$x\in e$
, and
 $\xi _1$
is at angle
$\xi _1$
is at angle
 $\frac {\pi }{2}$
from e and
$\frac {\pi }{2}$
from e and -
• the geodesic
 $yx$
from the definition of
$yx$
from the definition of
 $\xi _1\in F(\xi _0)$
ends in
$\xi _1\in F(\xi _0)$
ends in
 $T_b$
.
$T_b$
.
Note that
![]() $V^{ab}$
has positive Markov measure. Thus, by the Poincaré recurrence (see, e.g. [Reference WaltersWal82, Theorem 1.4]), there is
$V^{ab}$
has positive Markov measure. Thus, by the Poincaré recurrence (see, e.g. [Reference WaltersWal82, Theorem 1.4]), there is
![]() $(\xi _i)_i\in V^{ab}$
and
$(\xi _i)_i\in V^{ab}$
and
![]() $j>0$
with
$j>0$
with
![]() $(\xi _{i-j})_i\in GV^{ab}$
. Consequently, there is a geodesic
$(\xi _{i-j})_i\in GV^{ab}$
. Consequently, there is a geodesic
![]() $\gamma ^{ab}$
in
$\gamma ^{ab}$
in
![]() $Z\setminus Z^0$
starting perpendicularly to e in
$Z\setminus Z^0$
starting perpendicularly to e in
![]() $T_a$
and ending perpendicularly to a translate
$T_a$
and ending perpendicularly to a translate
![]() $fe$
in
$fe$
in
![]() $fT_b$
, for some
$fT_b$
, for some
![]() $f\in G$
.
$f\in G$
.
Denote by
![]() $a, fb$
the endpoints of
$a, fb$
the endpoints of
![]() $\gamma ^{ab}$
. Let
$\gamma ^{ab}$
. Let
![]() $I^{ab}$
be the domain of the isometric embedding
$I^{ab}$
be the domain of the isometric embedding
![]() $\gamma ^{ab}\colon I^{ab}\to Z\setminus Z^0$
. Analogously, there is a geodesic
$\gamma ^{ab}\colon I^{ab}\to Z\setminus Z^0$
. Analogously, there is a geodesic
![]() $\gamma ^{ca}\colon I^{ca}\to Z\setminus Z^0$
starting perpendicularly to e in
$\gamma ^{ca}\colon I^{ca}\to Z\setminus Z^0$
starting perpendicularly to e in
![]() $T_c$
and ending perpendicularly to a translate
$T_c$
and ending perpendicularly to a translate
![]() $ge$
in
$ge$
in
![]() $gT_a$
, with endpoints
$gT_a$
, with endpoints
![]() $c, a'$
, for some
$c, a'$
, for some
![]() $g\in G$
. Finally, there is a geodesic
$g\in G$
. Finally, there is a geodesic
![]() $\gamma ^{bc}\colon I^{bc}\to Z\setminus Z^0$
starting perpendicularly to
$\gamma ^{bc}\colon I^{bc}\to Z\setminus Z^0$
starting perpendicularly to
![]() $ge$
in
$ge$
in
![]() $T_b$
and ending perpendicularly to a translate
$T_b$
and ending perpendicularly to a translate
![]() $f'ge$
in
$f'ge$
in
![]() $f'gT_c$
, with endpoints
$f'gT_c$
, with endpoints
![]() $b', f'c'$
, for some
$b', f'c'$
, for some
![]() $f'\in G$
. Let
$f'\in G$
. Let
![]() $\gamma \colon I\to e$
be the shortest geodesic in e containing all
$\gamma \colon I\to e$
be the shortest geodesic in e containing all
![]() $a,b,c$
in its image (possibly I is a single point), and let
$a,b,c$
in its image (possibly I is a single point), and let
![]() $\gamma '\colon I'\to ge$
be the shortest geodesic in
$\gamma '\colon I'\to ge$
be the shortest geodesic in
![]() $ge$
containing all
$ge$
containing all
![]() $a',b',c'$
in its image.
$a',b',c'$
in its image.
Let
![]() $\Gamma $
be the metric graph obtained in the following way. We start from the disjoint union of the five intervals
$\Gamma $
be the metric graph obtained in the following way. We start from the disjoint union of the five intervals
![]() $I^{ab},I^{ca},I^{bc},I,I'$
, and we identify (see Figure 6):
$I^{ab},I^{ca},I^{bc},I,I'$
, and we identify (see Figure 6):
-
• points of I and
 $I^{ab}$
mapping to a under
$I^{ab}$
mapping to a under
 $\gamma $
and
$\gamma $
and
 $\gamma ^{ab}$
,
$\gamma ^{ab}$
, -
• points of I and
 $I^{ca}$
mapping to c under
$I^{ca}$
mapping to c under
 $\gamma $
and
$\gamma $
and
 $\gamma ^{ca}$
,
$\gamma ^{ca}$
, -
• points of
 $I'$
and
$I'$
and
 $I^{ca}$
mapping to
$I^{ca}$
mapping to
 $a'$
under
$a'$
under
 $\gamma '$
and
$\gamma '$
and
 $\gamma ^{ca}$
and
$\gamma ^{ca}$
and -
• points of
 $I'$
and
$I'$
and
 $I^{bc}$
mapping to
$I^{bc}$
mapping to
 $b'$
under
$b'$
under
 $\gamma '$
and
$\gamma '$
and
 $\gamma ^{bc}$
.
$\gamma ^{bc}$
.
Note that
![]() $\Gamma $
admits the map
$\Gamma $
admits the map
![]() $\varphi \colon \Gamma \to Z$
that is the quotient of
$\varphi \colon \Gamma \to Z$
that is the quotient of
![]() $\gamma ^{ab}\sqcup \gamma ^{ca}\sqcup \gamma ^{bc}\sqcup \gamma \sqcup \gamma '$
. Let
$\gamma ^{ab}\sqcup \gamma ^{ca}\sqcup \gamma ^{bc}\sqcup \gamma \sqcup \gamma '$
. Let
![]() $s,t,s',t'$
, be the points in
$s,t,s',t'$
, be the points in
![]() $I,I^{ab},I',I^{bc}$
mapping under
$I,I^{ab},I',I^{bc}$
mapping under
![]() $\varphi $
to
$\varphi $
to
![]() $b, fb, c',f'c'$
, respectively.
$b, fb, c',f'c'$
, respectively.

Figure 6 The graph
![]() $\Gamma $
.
$\Gamma $
.
Let
![]() $F_2$
be the free group on two generators
$F_2$
be the free group on two generators
![]() $h,h'$
, and let
$h,h'$
, and let
![]() $\widehat \Gamma $
be the quotient of the graph
$\widehat \Gamma $
be the quotient of the graph
![]() $F_2\times \Gamma $
(which is the disjoint union of
$F_2\times \Gamma $
(which is the disjoint union of
![]() $F_2$
copies of
$F_2$
copies of
![]() $\Gamma $
) by the relations
$\Gamma $
) by the relations
![]() $w\times t\sim wh\times s, w\times t'\sim wh'\times s'$
, for all
$w\times t\sim wh\times s, w\times t'\sim wh'\times s'$
, for all
![]() $w\in F_2$
. Note that
$w\in F_2$
. Note that
![]() $\widehat \Gamma $
is a tree with a free action of
$\widehat \Gamma $
is a tree with a free action of
![]() $F_2$
. Let
$F_2$
. Let
![]() $\varphi _*\colon F_2 \to G$
be the homomorphism mapping
$\varphi _*\colon F_2 \to G$
be the homomorphism mapping
![]() $h,h'$
to
$h,h'$
to
![]() $f,f'$
, respectively. Then
$f,f'$
, respectively. Then
![]() $\varphi $
extends to a
$\varphi $
extends to a
![]() $\varphi _*$
-equivariant map
$\varphi _*$
-equivariant map
![]() $\widehat \varphi \colon \widehat \Gamma \to Z$
mapping each
$\widehat \varphi \colon \widehat \Gamma \to Z$
mapping each
![]() $w\times r\in F_2\times \Gamma $
to
$w\times r\in F_2\times \Gamma $
to
![]() $\varphi _*(w)\varphi (r)\in Z$
.
$\varphi _*(w)\varphi (r)\in Z$
.
Let w be a nontrivial element of
![]() $F_2$
, and let
$F_2$
, and let
![]() $\mathbb {R}_w$
be the axis for w in
$\mathbb {R}_w$
be the axis for w in
![]() $\widehat \Gamma $
. Pick
$\widehat \Gamma $
. Pick
![]() $p\in \mathbb {R}_w$
an endpoint of a translate of one of
$p\in \mathbb {R}_w$
an endpoint of a translate of one of
![]() $I^{ab},I^{ca},I^{bc}$
contained in
$I^{ab},I^{ca},I^{bc}$
contained in
![]() $\mathbb {R}_w$
. Let
$\mathbb {R}_w$
. Let
![]() $I_w\subset \mathbb {R}_w$
be the interval between p and
$I_w\subset \mathbb {R}_w$
be the interval between p and
![]() $wp$
, and let
$wp$
, and let
![]() $\gamma _w\colon I_w\to Z$
be the restriction of
$\gamma _w\colon I_w\to Z$
be the restriction of
![]() $\widehat \varphi $
to
$\widehat \varphi $
to
![]() $I_w$
. Since
$I_w$
. Since
![]() $T_a,T_b,T_c,$
were distinct, we have that
$T_a,T_b,T_c,$
were distinct, we have that
![]() $\gamma _w$
is a sheared geodesic. By Proposition 8.2, we have
$\gamma _w$
is a sheared geodesic. By Proposition 8.2, we have
![]() $\widehat \varphi (p)\neq \widehat \varphi (wp)=\varphi _*(w)\widehat \varphi (p)$
, and, consequently,
$\widehat \varphi (p)\neq \widehat \varphi (wp)=\varphi _*(w)\widehat \varphi (p)$
, and, consequently,
![]() $\varphi _*(w)$
is nontrivial. Thus,
$\varphi _*(w)$
is nontrivial. Thus,
![]() $\varphi _*$
is injective, and so G contains a nonabelian free group.
$\varphi _*$
is injective, and so G contains a nonabelian free group.
Acknowledgments
We thank Werner Ballmann, Martin Bridson, Florestan Brunck, Pierre-Emmanuel Caprace, Koji Fujiwara, Stéphane Lamy, Paul Tee and the referee for helpful remarks. DO and PP were partially supported by (Polish) Narodowe Centrum Nauki, UMO-2018/30/M/ST1/00668. PP was partially supported by National Science and Engineering Research Council of Canada and American Mathematical Society.
Conflict of Interest
The authors have no conflict of interest to declare.