No CrossRef data available.
Published online by Cambridge University Press: 16 July 2009
Bennett functions 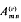 , (h, k), defined below and elsewhere, have been used extensively in Fourier analysing the output of certain devices such as rectifiers, limiters and other instantaneous modulators responding to a two-frequency input for which the output at time t depends only on the device input–output characteristic Y = Y(X) and the input at time t. Here, with the aid of a new set of modified Bennett functions
, (h, k), defined below and elsewhere, have been used extensively in Fourier analysing the output of certain devices such as rectifiers, limiters and other instantaneous modulators responding to a two-frequency input for which the output at time t depends only on the device input–output characteristic Y = Y(X) and the input at time t. Here, with the aid of a new set of modified Bennett functions 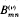 , (h, k), these methods are extended to solve the same problems for non-instantaneous bang-bang controls with multivalued input–output characteristics Y = Y(X) and hence having memory.
, (h, k), these methods are extended to solve the same problems for non-instantaneous bang-bang controls with multivalued input–output characteristics Y = Y(X) and hence having memory.