Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T15:52:04.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact convex sets of the plane and probability theory∗

Published online by Cambridge University Press:  29 October 2014

Jean-François Marckert  and
David Renault
Jean-François Marckert
Affiliation:
CNRS, LaBRI, Université de Bordeaux, 351 cours de la Libération, 33405 Talence cedex, France. [email protected]; [email protected]
David Renault
Affiliation:
CNRS, LaBRI, Université de Bordeaux, 351 cours de la Libération, 33405 Talence cedex, France. [email protected]; [email protected]
Get access

Abstract

The Gauss−Minkowskicorrespondence in ℝ2 states the existence of a homeomorphism between theprobability measures μ on [0,2π] such that \hbox{$\int_0^{2\pi} {\rm e}^{ix}{\rm d}\mu(x)=0$}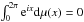∫02πeixdμ(x)=0 and the compact convex sets (CCS) of the plane withperimeter 1. In this article, we bring out explicit formulas relating the border of a CCSto its probability measure. As a consequence, we show that some natural operations on CCS– for example, the Minkowski sum – have natural translations in terms of probabilitymeasure operations, and reciprocally, the convolution of measures translates into a newnotion of convolution of CCS. Additionally, we give a proof that a polygonal curveassociated with a sample of n random variables (satisfying \hbox{$\int_0^{2\pi} {\rm e}^{ix}{\rm d}\mu(x)=0$}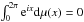∫02πeixdμ(x)=0) converges to a CCS associated with μ at speed √n, a result much similar to the convergence of theempirical process in statistics. Finally, we employ this correspondence to present modelsof smooth random CCS and simulations.

Keywords

Random convex setssymmetrisationweak convergenceMinkowski sum
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 18 , 2014 , pp. 854 - 880
Copyright
© EDP Sciences, SMAI 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bárány, I., Sylvester’s question: The probability that n points are in convex position. Ann. Probab. 27 (1999) 2020–2034. Google Scholar
I. Bárány, Random polytopes, convex bodies and approximation, in Stochastic Geometry, Vol. 1892 of Lect. Notes Math. Springer Berlin/Heidelberg (2007) 77–118.
Bárány, I. and Vershik, A.M., On the number of convex lattice polytopes. Geom. Func. Anal. 2 (1992) 381–393. Google Scholar
P. Billingsley, Convergence of probability measures. Wiley Series in Probability and Statistics: Probability and Statistics, 2nd edition. A Wiley-Interscience Publication. John Wiley & Sons Inc., New York (1999).
O. Bodini, Ph. Duchon, A. Jacquot and L. Mutafchiev, Asymptotic analysis and random sampling of digitally convex polyominoes. In Proc. of the 17th IAPR international conference on Discrete Geometry for Computer Imagery, DGCI’13. Springer-Verlag, Berlin, Heidelberg (2013) 95–106.
Bogachev, L.V. and Zarbaliev, S.M., Universality of the limit shape of convex lattice polygonal lines. Ann. Probab. 39 (1992) 2271–2317. Google Scholar
C. Buchta, On the boundray structure of the convex hull of random points. Adv. Geom. (2012). Available at: http://www.uni-salzburg.at/pls/portal/docs/1/1739190.PDF.
H. Busemann, Convex Surfaces. Interscience. New York (1958).
Calka, P., Precise formulae for the distributions of the principal geometric characteristics of the typical cells of a two-dimensional poisson-voronoi tessellation and a poisson line process. Adv. Appl. Probab. 35 (2003) 551–562. Available at http://www.univ-rouen.fr/LMRS/Persopage/Calka/publications.html. Google Scholar
R.M. Dudley, Real Analysis and Probability. Cambridge Studies in Advanced Mathematics. Cambridge University Press (2002).
W. Feller, An introduction to probability theory and its applications. Vol. II. 2nd edition. John Wiley & Sons Inc., New York (1971).
Hurwitz, M.A., Sur le problème des isopérimètres. C. R. Acad. Sci. Paris 132 (1901) 401–403. Google Scholar
Hurwitz, M.A., Sur quelques applications géométriques des séries de Fourier. Annales Scientifiques de l’École Normale supérieure, 19 (1902) 357–408. Available at http://archive.numdam.org/article/ASENS˙1902˙3˙19˙˙357˙0.pdf. Google Scholar
B. Klartag, On John-type ellipsoids, in Geometric aspects of functional analysis, vol. 1850 of Lect. Notes Math. Springer, Berlin (2004) 149–158.
D.E. Knuth, Axioms and hulls. Vol. 606 of Lect. Notes Comput. Sci. Springer-Verlag, Berlin (1992). Available at: http://www-cs-faculty.stanford.edu/˜uno/aah.html.
Lévy, P., L’addition des variables aléatoires définies sur un circonférence. Bull. Soc. Math. France 67 (1939) 1–41. Available at http://archive.numdam.org/article/BSMF˙1939˙˙67˙˙1˙0.pdf. Google Scholar
J.-F. Marckert, Probability that n random points in a disk are in convex position. Available at http://arxiv.org/abs/1402.3512 (2014).
M. Moszyńska, Selected Topics in Convex Geometry. Birkhäuser (2006).
V.V. Petrov, Sums of independent random variables. Translated from the Russian by A.A. Brown. Band 82, Ergebnisse der Mathematik und ihrer Grenzgebiete. Springer-Verlag, New York (1975).
A.V. Pogorelov, Extrinsic geometry of convex surfaces. American Mathematical Society, Providence, R.I. (1973). Translated from the Russian by Israel Program for Scientific Translations, in vol. 35 Translations of Mathematical Monographs.
G. Pólya, Isoperimetric Inequalities in Mathematical Physics. Ann. Math. Stud. Kraus (1965).
W. Rudin, Real and Complex Analysis, 3rd edn. McGraw-Hill International Editions (1987).
R. Schneider, Convex Bodies: The Brunn−Minkowski Theory. Cambridge University Press (1993).
Sinai, Ya.G., Probabilistic approach to the analysis of statistics for convex polygonal lines. Functional Anal. Appl. 28 (1994) 1. Google Scholar
J.J. Sylvester, On a special class of questions on the theory of probabilities. Birmingham British Assoc. Rept. (1865) 8–9.
G. Szegö, Orthogonal polynomials. Colloquium Publications, 4th edition. American Mathematical Society (1939).
Valtr, P., Probability that n random points are in convex position. Discr. Comput. Geom. 13 (1995) 637–643. Google Scholar
Valtr, P., The probability that n random points in a triangle are in convex position. Combinatorica 16 (1996) 567–573. Google Scholar
Vershik, A. and Zeitouni, O., large deviations in the geometry of convex lattice polygons. Israel J. Math. 109 (1999) 13–27. Google Scholar
R.J.G. Wilms, Fractional parts of random variables. Limit theorems and infinite divisibility, Dissertation. Technische Universiteit Eindhoven, Eindhoven (1994).