Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jayawardana, Kavinda
Mordacq, Christelle
Ortner, Christoph
and
Park, Harold S.
2013.
An analysis of the boundary layer in the 1D surface Cauchy–Born model.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 47,
Issue. 1,
p.
109.
Mainini, Edoardo
and
Stefanelli, Ulisse
2014.
Crystallization in Carbon Nanostructures.
Communications in Mathematical Physics,
Vol. 328,
Issue. 2,
p.
545.
Rosakis, Phoebus
2014.
Continuum surface energy from a lattice model.
Networks & Heterogeneous Media,
Vol. 9,
Issue. 3,
p.
453.
Kitavtsev, Georgy
Luckhaus, Stephan
and
Rüland, Angkana
2015.
Surface energies arising in microscopic modeling of martensitic transformations.
Mathematical Models and Methods in Applied Sciences,
Vol. 25,
Issue. 04,
p.
647.
Hudson, T.
and
Ortner, C.
2015.
Analysis of Stable Screw Dislocation Configurations in an Antiplane Lattice Model.
SIAM Journal on Mathematical Analysis,
Vol. 47,
Issue. 1,
p.
291.
Braides, A.
and
Gelli, M.S.
2016.
Asymptotic analysis of microscopic impenetrability constraints for atomistic systems.
Journal of the Mechanics and Physics of Solids,
Vol. 96,
Issue. ,
p.
235.
Braun, Julian
and
Schmidt, Bernd
2016.
Existence and convergence of solutions of the boundary value problem in atomistic and continuum nonlinear elasticity theory.
Calculus of Variations and Partial Differential Equations,
Vol. 55,
Issue. 5,
Braides, Andrea
and
Solci, Margherita
2016.
Asymptotic analysis of Lennard-Jones systems beyond the nearest-neighbour setting: A one-dimensional prototypical case.
Mathematics and Mechanics of Solids,
Vol. 21,
Issue. 8,
p.
915.
Braides, Andrea
and
Gelli, Maria Stella
2017.
Analytical treatment for the asymptotic analysis of microscopic impenetrability constraints for atomistic systems.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 51,
Issue. 5,
p.
1903.
Binder, Andrew J.
Luskin, Mitchell
and
Ortner, Christoph
2017.
Analysis of a Predictor-Corrector Method for Computationally Efficient Modeling of Surface Effects in 1D.
Multiscale Modeling & Simulation,
Vol. 15,
Issue. 2,
p.
892.
Braun, Julian
2017.
Connecting Atomistic and Continuous Models of Elastodynamics.
Archive for Rational Mechanics and Analysis,
Vol. 224,
Issue. 3,
p.
907.
Buze, Maciej
Hudson, Thomas
and
Ortner, Christoph
2019.
Analysis of an atomistic model for anti-plane fracture.
Mathematical Models and Methods in Applied Sciences,
Vol. 29,
Issue. 13,
p.
2469.
Mainini, Edoardo
and
Schmidt, Bernd
2020.
Maximal Fluctuations Around the Wulff Shape for Edge-Isoperimetric Sets in $$\varvec{{\mathbb {Z}}^d}$$: A Sharp Scaling Law.
Communications in Mathematical Physics,
Vol. 380,
Issue. 2,
p.
947.
Buze, Maciej
2021.
Atomistic modelling of near-crack-tip plasticity
*
.
Nonlinearity,
Vol. 34,
Issue. 7,
p.
4503.
Xie, You
Mao, Huiqi
Yao, Angela
and
Thuerey, Nils
2022.
TemporalUV: Capturing Loose Clothing with Temporally Coherent UV Coordinates.
p.
3440.
Dedkova, A. A.
Glagolev, P. Yu.
Gusev, E. E.
Dyuzhev, N. A.
Kireev, V. Yu.
Lychev, S. A.
and
Tovarnov, D. A.
2024.
Peculiarities of Deformation of Round Thin-Film Membranes and Experimental Determination of Their Effective Characteristics.
Technical Physics,
Vol. 69,
Issue. 2,
p.
201.
Friedrich, Manuel
Seitz, Manuel
and
Stefanelli, Ulisse
2024.
Discrete-to-continuum linearization in atomistic dynamics.
Discrete and Continuous Dynamical Systems,
Vol. 0,
Issue. 0,
p.
0.
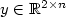 characterizes the particle positions. The mainfocus is the asymptotic analysis of the ground state energy as ntends to infinity. We show in a suitable scaling regime where theenergy is essentially quadratic that the energy minimum of E (n)admits an asymptotic expansion involving fractional powers of n:
characterizes the particle positions. The mainfocus is the asymptotic analysis of the ground state energy as ntends to infinity. We show in a suitable scaling regime where theenergy is essentially quadratic that the energy minimum of E (n)admits an asymptotic expansion involving fractional powers of n: