Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T08:59:54.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Cogrowth for group actions with strongly contracting elements

Part of: Special aspects of infinite or finite groups Smooth dynamical systems: general theory

Published online by Cambridge University Press:  04 December 2018

GOULNARA N. ARZHANTSEVA  and
CHRISTOPHER H. CASHEN Open the ORCID record for CHRISTOPHER H. CASHEN [Opens in a new window]
GOULNARA N. ARZHANTSEVA
Affiliation:
Universität Wien, Fakultät für Mathematik, Oskar-Morgenstern-Platz 1, 1090 Wien, Österreich email [email protected], [email protected]
CHRISTOPHER H. CASHEN
Affiliation:
Universität Wien, Fakultät für Mathematik, Oskar-Morgenstern-Platz 1, 1090 Wien, Österreich email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 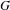$G$ be a group acting properly by isometries and with a strongly contracting element on a geodesic metric space. Let 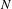$N$ be an infinite normal subgroup of 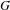$G$ and let 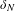$\unicode[STIX]{x1D6FF}_{N}$ and 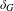$\unicode[STIX]{x1D6FF}_{G}$ be the growth rates of 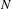$N$ and 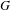$G$ with respect to the pseudo-metric induced by the action. We prove that if 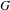$G$ has purely exponential growth with respect to the pseudo-metric, then 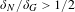$\unicode[STIX]{x1D6FF}_{N}/\unicode[STIX]{x1D6FF}_{G}>1/2$. Our result applies to suitable actions of hyperbolic groups, right-angled Artin groups and other CAT(0) groups, mapping class groups, snowflake groups, small cancellation groups, etc. This extends Grigorchuk’s original result on free groups with respect to a word metric and a recent result of Matsuzaki, Yabuki and Jaerisch on groups acting on hyperbolic spaces to a much wider class of groups acting on spaces that are not necessarily hyperbolic.

Keywords

cogrowthexponential growthcontracting elementmapping class groupsCAT(0) groups

MSC classification

Primary: 20F69: Asymptotic properties of groups 37C35: Orbit growth
Secondary: 20F65: Geometric group theory 20F67: Hyperbolic groups and nonpositively curved groups 20F36: Braid groups; Artin groups
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 7 , July 2020 , pp. 1738 - 1754
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arzhantseva, G. N., Cashen, C. H., Gruber, D. and Hume, D.. Negative curvature in graphical small cancellation groups. Groups Geom. Dyn. to appear.Google Scholar
Arzhantseva, G. N., Cashen, C. H. and Tao, J.. Growth tight actions. Pacific J. Math. 278(1) (2015), 1–49.Google Scholar
Bestvina, M., Bromberg, K. and Fujiwara, K.. Constructing group actions on quasi-trees and applications to mapping class groups. Publ. Math. Inst. Hautes Études Sci. 122(1) (2015), 1–64.Google Scholar
Bestvina, M., Bromberg, K., Fujiwara, K. and Sisto, A.. Acylindrical actions on projection complexes. Preprint, 2017, arXiv:1711.08722v1.Google Scholar
Bonfert-Taylor, P., Matsuzaki, K. and Taylor, E. C.. Large and small covers of a hyperbolic manifold. J. Geom. Anal. 22(2) (2012), 455–470.Google Scholar
Brooks, R.. The bottom of the spectrum of a Riemannian covering. J. Reine Angew. Math. 357 (1985), 101–114.Google Scholar
Champetier, C.. Cocroissance es groupes à petite simplification. Bull. Lond. Math. Soc. 25(5) (1993), 438–444.Google Scholar
Cohen, J. M.. Cogrowth and amenability of discrete groups. J. Funct. Anal. 48(3) (1982), 301–309.Google Scholar
Coornaert, M.. Mesures de Patterson–Sullivan sur le bord d’un espace hyperbolique au sens de Gromov. Pacific J. Math. 159(2) (1993), 241–270.Google Scholar
Coulon, R., Dal’Bo, F. and Sambusetti, A.. Growth gap in hyperbolic groups and amenability. Preprint, 2017, arXiv:1709.07287v1.Google Scholar
Dal’Bo, F., Peigné, M., Picaud, J.-C. and Sambusetti, A.. On the growth of quotients of Kleinian groups. Ergod. Th. & Dynam. Sys. 31(3) (2011), 835–851.Google Scholar
Dougall, R. and Sharp, R.. Amenability, critical exponents of subgroups and growth of closed geodesics. Math. Ann. 365(3–4) (2016), 1359–1377.Google Scholar
Grigorchuk, R. I.. Symmetrical random walks on discrete groups. Multicomponent Random Systems (Advances in Probability and Related Topics, 6). Dekker, New York, 1980, pp. 285–325.Google Scholar
Grigorchuk, R. and de la Harpe, P.. On problems related to growth, entropy, and spectrum in group theory. J. Dyn. Control Syst. 3(1) (1997), 51–89.Google Scholar
de la Harpe, P.. Topics in Geometric Group Theory (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 2000.Google Scholar
Jaerisch, J.. A lower bound for the exponent of convergence of normal subgroups of Kleinian groups. J. Geom. Anal. 25(1) (2015), 298–305.Google Scholar
Jaerisch, J. and Matsuzaki, K.. Growth and cogrowth of normal subgroups of a free group. Proc. Amer. Math. Soc. 145(10) (2017), 4141–4149.Google Scholar
Matsuzaki, K.. Growth and cogrowth tightness of Kleinian and hyperbolic groups. Geometry and Analysis of Discrete Groups and Hyperbolic Spaces (RIMS Kôkyûroku Bessatsu, B66). Eds. Fujii, M., Kawazumi, N. and Ohshika, K.. Research Institute for Mathematical Sciences, Kyoto, 2017, pp. 21–36.Google Scholar
Matsuzaki, K., Yabuki, Y. and Jaerisch, J.. Normalizer, divergence type and Patterson measure for discrete groups of the Gromov hyperbolic space. Preprint, 2015, arXiv:1511.02664v1.Google Scholar
Ollivier, Y.. Cogrowth and spectral gap of generic groups. Ann. Inst. Fourier (Grenoble) 55(1) (2005), 289–317.Google Scholar
Roblin, T.. Un théorème de Fatou pour les densités conformes avec applications aux revêtements Galoisiens en courbure négative. Israel J. Math. 147 (2005), 333–357.Google Scholar
Roblin, T. and Tapie, S.. Exposants critiques et moyennabilité. Géométrie Ergodique (Monographs of L’Enseignement Mathématique, 43). L’Enseignement Mathématique, Geneva, 2013, pp. 61–92.Google Scholar
Shalom, Y.. Rigidity, unitary representations of semisimple groups, and fundamental groups of manifolds with rank one transformation group. Ann. of Math. (2) 152(1) (2000), 113–182.Google Scholar
Sullivan, D.. Related aspects of positivity in Riemannian geometry. J. Differential Geom. 25(3) (1987), 327–351.Google Scholar
Yang, W.. Statistically convex-cocompact actions of groups with contracting elements. Int. Math. Res. Not. to appear.Google Scholar