Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T10:40:14.872Z Has data issue: false hasContentIssue false
  • English
  • Français

Bernoulli shifts of the same entropy are finitarily and unilaterally isomorphic

Published online by Cambridge University Press:  19 September 2008

Andrés Del Junco
Andrés Del Junco
Affiliation:
Department of Mathematics, University of Toronto, Toronto, M5S 1A1, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p = {p1,  , pn} and q = {qi,  , qm} be finite probability vectors, each having at least three non-zero components, such that 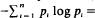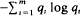. Let C = {1,  , n}, D = {1,  , m} and let (Cℤ, pℤ, σ) and (Dℤ, qℤ, σ) be the corresponding Bernoulli shifts. Then there exists an isomorphism φ between these shifts such that for a.a. x ∈ Cℤ σ(x)(0) is determined by finitely many of the future co-ordinates x(0), x(1),   and for a. a.y ∈ Dℤφ−1(y)(0) is determined by finitely many of the co-ordinates   y(−1), y(0), y(1),  .

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 10 , Issue 4 , December 1990 , pp. 687 - 715
Copyright
Copyright © Cambridge University Press 1990

References

REFERENCES

[B, R]Burton, R. & Rothstein, A.. Isomorphism theorem in ergodic theory. Preprint.Google Scholar
[J]del Junco, A.. Finitary codes between one-sided Bernoulli shifts. Ergod. Th. & Dynam. Sys. 1 (1981), 285–301.CrossRefGoogle Scholar
[K, S]Keane, M. & Smorodinsky, M.. Bernoulli shifts of the same entropy are finitarily isomorphic. Ann. Math. 109 (1979), 397–406.CrossRefGoogle Scholar
[M]Meshalkin, L.. A case of isomorphy of Bernoulli schemes. Dokl. Akad. Nauk SSSR 128 (1959), 41–44.Google Scholar
[O]Ornstein, D.. Ergodic Theory, Randomness and Dynamical Systems. New Haven and London, Yale University Press (1974).Google Scholar
[O, W]Ornstein, D. & Weiss, B.. Unilateral codings of Bernoulli systems. Israel J. Math. 21 (1975), 159–166.CrossRefGoogle Scholar
[P]Propp, J.. PhD dissertation, University of California, Berkeley (1987).Google Scholar
[S]Sinai, Ja. G.. A weak isomorphism of transformations with an invariant measure. Dokl. Akad. Nauk SSSR 147 (1962), 797–800.Google Scholar
[W]Walters, P.. Some results on the classification of non-invertible measure-preserving transformations. Lecture Notes in Mathematics 318, pp 266–276. Springer Verlag, Berlin (1973).Google Scholar