Article contents
Approximations of continuous functions by squares
Published online by Cambridge University Press: 19 September 2008
Abstract
Let C denote the space of continuous functions mapping [0,1] into itself and endowed with the sup metric. It has been shown that C2 = {f ∘ f: ∈ C} is an analytic but non-Borel subset of C. This implies that there is no simple geometric characterization for a function being a square. In this paper we consider the problem of characterizing those functions which can be approximated by squares. In the first section we prove that any continuous function mapping a closed proper subset of [0,1 ] into [0,1 ] can be extended to a square. In particular this shows that C2 is Lp dense in C. On the other hand, C2 does not contain a ball when C is endowed with the sup metric. In the second section we prove that no strictly decreasing function can be uniformly approximated by squares, although the distance between the class of strictly decreasing functions and C2 is zero. In the last section we investigate the function f(x) = 1 − x and show that 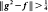 for every g ∈ C and that ¼ cannot be improved.
for every g ∈ C and that ¼ cannot be improved.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1990
References
REFERENCE
- 5
- Cited by


