Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T02:54:21.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Toeplitz flows and their ordered K-theory

Published online by Cambridge University Press:  11 February 2015

SIRI-MALÉN HØYNES
SIRI-MALÉN HØYNES*
Affiliation:
Department of Mathematical Sciences, Norwegian University of Science and Technology (NTNU), N-7034 Trondheim, Norway email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

To a Toeplitz flow 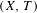$(X,T)$ we associate an ordered 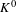$K^{0}$-group, denoted 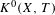$K^{0}(X,T)$, which is order isomorphic to the 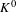$K^{0}$-group of the associated (non-commutative) 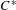$C^{\ast }$-crossed product 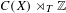$C(X)\rtimes _{T}\mathbb{Z}$. However, 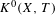$K^{0}(X,T)$ can be defined in purely dynamical terms, and it turns out to be a complete invariant for (strong) orbit equivalence. We characterize the 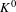$K^{0}$-groups that arise from Toeplitz flows 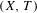$(X,T)$ as exactly those simple dimension groups 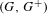$(G,G^{+})$ that contain a non-cyclic subgroup 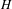$H$ of rank one that intersects $G^{+}$ non-trivially. Furthermore, the Bratteli diagram realization of 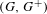$(G,G^{+})$ can be chosen to have the ERS property, i.e. the incidence matrices of the Bratteli diagram have equal row sums. We also prove that for any Choquet simplex 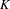$K$ there exists an uncountable family of pairwise non-orbit equivalent Toeplitz flows 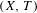$(X,T)$ such that the set of $T$-invariant probability measures 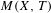$M(X,T)$ is affinely homeomorphic to 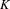$K$, where the entropy 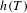$h(T)$ may be prescribed beforehand. Furthermore, the analogous result is true if we substitute strong orbit equivalence for orbit equivalence, but in that case we can actually prescribe both the entropy and the maximal equicontinuous factor of 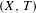$(X,T)$. Finally, we present some interesting concrete examples of dimension groups associated to Toeplitz flows.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 6 , September 2016 , pp. 1892 - 1921
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackadar, B.. K-theory for Operator Algebras (Mathematical Sciences Research Institute Publications, 5) . Springer, New York, 1986.CrossRefGoogle Scholar
Boyle, M. and Tomiyama, J.. Bounded topological orbit equivalence and C∗ -algebras. J. Math. Soc. Japan 50(2) (1998), 317–329.Google Scholar
Cortez, M. I. and Petite, S.. Invariant measures and orbit equivalence for generalized Toeplitz subshifts. Groups Geom. Dyn., accepted for publication. Preprint, arXiv:1106.4280.Google Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Algebraic and Topological Dynamics (Contemporary Mathematics, 385) . Eds. Kolyada, S., Manin, Y. and Ward, T.. American Mathematical Society, Providence, RI, 2005, pp. 7–38.Google Scholar
Downarowicz, T. and Durand, F.. Factors of Toeplitz flows and other almost 1–1 extensions over group rotations. Math. Scand. 90 (2002), 57–72.CrossRefGoogle Scholar
Durand, F., Host, B. and Skau, C. F.. Substitutional dynamical systems, Bratteli diagrams and dimension groups. Ergod. Th. & Dynam. Sys. 19 (1999), 995–1035.CrossRefGoogle Scholar
Downarowicz, T. and Maass, A.. Finite-rank Bratteli–Vershik diagrams are expansive. Ergod. Th. & Dynam. Sys. 28 (2008), 739–747.Google Scholar
Effros, E.. Dimensions and C∗ -Algebras (CBMS Regional Conference Series in Mathematics, 46) . American Mathematical Society, Providence, RI, 1981.CrossRefGoogle Scholar
Effros, E., Handelman, D. and Shen, C.. Dimension groups and their affine representations. Amer. J. Math. 102 (1980), 385–407.CrossRefGoogle Scholar
Fuchs, L.. Infinite Abelian Groups. Vol. II. Academic Press, New York, 1973.Google Scholar
Fack, T. and Marechal, O.. Sur la classification des symétries des C∗ -algébres UHF. Canad. J. Math. 31 (1979), 496–523.Google Scholar
Gottschalk, W. H. and Hedlund, G. A.. Topological Dynamics (American Mathematical Society Colloquium Publications, 36) . American Mathematical Society, Providence, RI, 1955.CrossRefGoogle Scholar
Glasner, E. and Host, B.. Extensions of Cantor minimal systems and dimension groups. J. Reine Angew. Math. 682 (2013), 207–243.CrossRefGoogle Scholar
Gjerde, R. and Johansen, Ø.. Bratteli–Vershik models for Cantor minimal systems: application to Toeplitz flows. Ergod. Th. & Dynam. Sys. 20 (2000), 1687–1710.Google Scholar
Giordano, T., Matui, H., Putnam, I. F. and Skau, C.. Orbit equivalence for Cantor minimal ℤ d -systems. Invent. Math. 179(1) (2010), 119–158.CrossRefGoogle Scholar
Giordano, T., Putnam, I. F. and Skau, C.. Topological orbit equivalence and C∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Giordano, T., Putnam, I. F. and Skau, C.. K-theory and asymptotic index for certain almost one-to-one factors. Math. Scand. 89 (2001), 297–319.Google Scholar
Glasner, E. and Weiss, B.. Weak orbit equivalence of Cantor minimal systems. Int. J. Math. 6 (1995), 569–579.Google Scholar
Handelman, D.. Equal column sum and equal row sum dimension group realizations. Preprint, arXiv:1301.2799.Google Scholar
Høynes, S.-M.. Finite-rank Bratteli–Vershik diagrams are expansive – a new proof. Preprint, 2014,arXiv:1411.3371.Google Scholar
Herman, R. H., Putnam, I. F. and Skau, C. F.. Ordered Bratteli diagrams, dimension groups, and topological dynamics. Int. J. Math. 3 (1992), 827–864.CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis I (Grundlehren der Mathematische Wissenschaften, 115) . Springer, Berlin, 1963.Google Scholar
Jacobs, K. and Keane, M.. 0–1-sequences of Toeplitz type. Z. Wahrscheinlichkeitsth. verw. Geb. 13 (1969), 123–131.Google Scholar
Kuratowski, K.. Topology. Vol. II. Academic Press, New York, 1968.Google Scholar
Martin, J. C.. Substitution minimal flows. Amer. J. Math. 93 (1971), 503–526.Google Scholar
Markley, N. G. and Paul, M. E.. Almost automorphic symbolic minimal sets without unique ergodicity. Israel J. Math. 34 (1979), 259–272.Google Scholar
Ormes, N. S.. Strong orbit realization for minimal homeomorphisms. J. Anal. Math. 71 (1997), 103–133.Google Scholar
Paul, M. E.. Construction of almost automorphic symbolic minimal flows. Appl. Gen. Topol. 6 (1976), 45–56.Google Scholar
Skau, C. F.. Ordered K-theory and minimal symbolic dynamical systems. Colloq. Math. 84–85 (2000), 203–227.Google Scholar
Sugisaki, F.. Toeplitz flows, ordered Bratteli diagrams and strong orbit equivalence. Ergod. Th. & Dynam. Sys. 21 (2001), 1867–1881.Google Scholar
Sugisaki, F.. On the subshift within a strong orbit equivalence class for minimal homeomorphisms. Ergod. Th. & Dynam. Sys. 27 (2007), 971–990.Google Scholar
Sugisaki, F.. Almost one-to-one extensions of Cantor minimal systems and order embeddings of simple dimension groups. Münster J. Math. 4 (2011), 141–169.Google Scholar
Toeplitz, O.. Beispiele zur Theorie der fastperiodischen Funktionen. Math. Ann. 98 (1928), 281–295.Google Scholar
Williams, S.. Toeplitz minimal flows which are not uniquely ergodic. Z. Wahrscheinlichkeitsth. verw. Geb. 67 (1984), 95–107.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar