Published online by Cambridge University Press: 21 October 2011
For a jointly measurable probability-preserving action τ:ℝD↷(X,μ) and a tuple of polynomial maps pi:ℝ→ℝD, i=1,2,…,k, the multiple ergodic averages 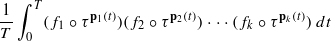 converge in L2(μ) as T→∞ for any f1,f2,…,fk∈L∞(μ). This confirms the continuous-time analog of the conjectured norm convergence of discrete polynomial multiple ergodic averages, which in its original formulation remains open in most cases. A proof of convergence can be given based on the idea of passing up to a sated extension of (X,μ,τ) in order to find a simple partially characteristic factor, similarly to the recent development of this idea for the study of related discrete-time averages, together with a new inductive scheme on tuples of polynomials. The new induction scheme becomes available upon changing the time variable in the above integral by some fractional power, and provides an alternative to Bergelson’s polynomial ergodic theorem induction, which has been the mainstay of positive results in this area in the past.
converge in L2(μ) as T→∞ for any f1,f2,…,fk∈L∞(μ). This confirms the continuous-time analog of the conjectured norm convergence of discrete polynomial multiple ergodic averages, which in its original formulation remains open in most cases. A proof of convergence can be given based on the idea of passing up to a sated extension of (X,μ,τ) in order to find a simple partially characteristic factor, similarly to the recent development of this idea for the study of related discrete-time averages, together with a new inductive scheme on tuples of polynomials. The new induction scheme becomes available upon changing the time variable in the above integral by some fractional power, and provides an alternative to Bergelson’s polynomial ergodic theorem induction, which has been the mainstay of positive results in this area in the past.