Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T09:58:55.488Z Has data issue: false hasContentIssue false
  • English
  • Français

Hausdorff and packing measure functions of self-similar sets: continuity and measurability

Published online by Cambridge University Press:  01 October 2008

L. OLSEN
L. OLSEN*
Affiliation:
Department of Mathematics, University of St. Andrews, St. Andrews, Fife KY16 9SS, Scotland, UK (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let N be an integer with N≥2 and let X be a compact subset of ℝd. If 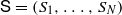is a list of contracting similarities Si:X→X, then we will write 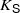for the self-similar set associated with 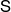, and we will write M for the family of all lists 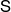satisfying the strong separation condition. In this paper we show that the maps (1)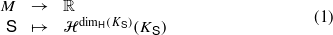and (2)are continuous; here 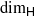denotes the Hausdorff dimension, ℋs denotes the s-dimensional Hausdorff measure and 𝒮s denotes the s-dimensional spherical Hausdorff measure. In fact, we prove a more general continuity result which, amongst other things, implies that the maps in (1) and (2) are continuous.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 5 , October 2008 , pp. 1635 - 1655
Copyright
Copyright © 2008 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ayer, E. and Strichartz, R.. Exact Hausdorff measure and intervals of maximum density for Cantor sets. Trans. Amer. Math. Soc. 351 (1999), 3725–3741.CrossRefGoogle Scholar
[2]Centore, P. M. and Vrscay, E. R.. Continuity of attractors and invariant measures for iterated function systems. Canad. Math. Bull. 37 (1994), 315–329.CrossRefGoogle Scholar
[3]Das, M.. Hausdorff measures, dimensions and mutual singularity. Trans. Amer. Math. Soc. to appear.Google Scholar
[4]Falconer, K. J.. Fractal Geometry – Mathematical Foundations and Applications. John Wiley & Sons, New York, 1990.CrossRefGoogle Scholar
[5]Hofbauer, F., Raith, P. and Steinberger, T.. Multifractal dimensions for invariant subsets of piecewise monotonic interval maps. Fund. Math. 176 (2003), 209–232.CrossRefGoogle Scholar
[6]Hutchinson, J.. Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981), 713–747.CrossRefGoogle Scholar
[7]Jung, S.-M.. On the Hausdorff measure of a class of self-similar sets. Real Anal. Exchange 24 (1998/99), 121–137.CrossRefGoogle Scholar
[8]Lewellen, G.. Self-similarity. Rocky Mountain J. Math. 23 (1993), 1023–1040.CrossRefGoogle Scholar
[9]Lee, H. and Baek, I. S.. Hausdorff measure of the scattered Cantor sets. Kyungpook Math. J. 35 (1996), 687–693.Google Scholar
[10]Marion, J.. Mesure de Hausdorff d’un fractal à similitude interne. Ann. Sci. Math. Québec 10 (1986), 51–84.Google Scholar
[11]Marion, J.. Mesures de Hausdorff d’ensembles fractals. Ann. Sci. Math. Québec 11 (1987), 111–132.Google Scholar
[12]Mattila, P.. On the structure of self-similar fractals. Ann. Acad. Sci. Fenn. Ser. A I Math. 7 (1982), 189–195.CrossRefGoogle Scholar
[13]McMullen, C.. Hausdorff dimension and conformal dynamics. II. Geometrically finite rational maps. Comment. Math. Helv. 75 (2000), 535–593.CrossRefGoogle Scholar
[14]Mauldin, D. and Urbański, M.. Graph Directed Markov Systems. Geometry and Dynamics of Limit Sets (Cambridge Tracts in Mathematics, 148). Cambridge University Press, Cambridge, 2003.CrossRefGoogle Scholar
[15]Olsen, L.. A multifractal formalism. Adv. Math. 116 (1995), 82–196.CrossRefGoogle Scholar
[16]Olsen, L.. Multifractal Geometry (Proceedings, Fractal Geometry and Stochastics II, Greifswald, Germany, August, 1998) (Progress in Probability, 46). Eds. C. Bandt, S. Graf and M. Zähle. Birkhäuser, Basel, 2000, pp. 1–37.Google Scholar
[17]Olsen, L.. Density theorems for Hausdorff and packing measures of self-similar sets. Aequationes Math. to appear.Google Scholar
[18]Peyriére, J.. Multifractal Measures (Proceedings of the NATO Advanced Study Institute on Probablistic and Stochastic Methods in Analysis with Applications, Il Ciocco) (NATO ASI Series, Series C: Mathematical and Physical Sciences, 372). Kluwer Academic Press, Dordrecht, 1992, pp. 175–186.Google Scholar
[19]Rivera-Letelier, J.. On the continuity of Hausdorff dimension of Julia sets and similarity between the Mandelbrot set and Julia sets. Fund. Math. 170 (2001), 287–317.CrossRefGoogle Scholar
[20]Raymond, X. S. and Tricot, C.. Packing regularity of sets in n-space. Math. Proc. Cambridge Philos. Soc. 103 (1988), 133–145.CrossRefGoogle Scholar
[21]Rogers, C. A.. Hausdorff Measures, 2nd edn. Cambridge University Press, London, New York, 1998.Google Scholar
[22]Salli, A.. Upper density properties of Hausdorff measures on fractals. Ann. Acad. Sci. Fenn. Ser. A I Math. Diss. 55 (1985).Google Scholar
[23]Spear, D.. Measures and self-similarity. Adv. Math. 91 (1992), 143–157.CrossRefGoogle Scholar
[24]Taylor, S. J. and Tricot, C.. Packing measure, and its evaluation for a Brownian path. Trans. Amer. Math. Soc. 288 (1985), 679–699.CrossRefGoogle Scholar
[25]Tricot, C.. Two definitions of fractional dimension. Math. Proc. Cambridge Philos. Soc. 91 (1982), 57–74.CrossRefGoogle Scholar
[26]Urbański, M. and Zinsmeister, M.. Continuity of Hausdorff dimension of Julia-Lavaurs sets as a function of the phase. Conform. Geom. Dyn. 5 (2001), 140–152.CrossRefGoogle Scholar
[27]Zhou, Z. and Wu, M.. The Hausdorff measure of a Sierpiński carpet. Sci. China Ser. A 42 (1999), 673–680.CrossRefGoogle Scholar