In this paper, we consider a 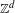$\mathbb{Z}^{d}$ extension of the well known fact that subshifts with only finitely many follower sets are sofic. As in Kass and Madden [A sufficient condition for non-soficness of higher-dimensional subshifts. Proc. Amer. Math. Soc.141 (2013), 3803–3816], we adopt a natural 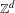$\mathbb{Z}^{d}$ analogue of a follower set called an extender set. The extender set of a finite word 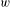$w$ in a 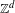$\mathbb{Z}^{d}$ subshift 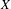$X$ is the set of all configurations of symbols on the rest of 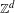$\mathbb{Z}^{d}$ which form a point of 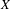$X$ when concatenated with 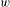$w$. 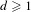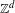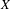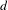As our main result, we show that for any $d\geq 1$ and any $\mathbb{Z}^{d}$ subshift $X$, if there exists $n$ so that the number of extender sets of words on a $d$-dimensional hypercube of side length $n$ is less than or equal to $n$, then 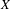$X$ is sofic. We also give an example of a non-sofic system for which this number of extender sets is 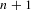$n+1$ for every $n$. We prove this theorem in two parts. 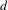First we show that if the number of extender sets of words on a $d$-dimensional hypercube of side length $n$ is less than or equal to $n$ for some $n$, then there is a uniform bound on the number of extender sets for words on any sufficiently large rectangular prism; to our knowledge, this result is new even for 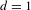$d=1$. We then show that such a uniform bound implies soficity. Our main result is reminiscent of the classical Morse–Hedlund theorem, which says that if $X$ is a $\mathbb{Z}$ subshift and there exists an $n$ such that the number of words of length $n$ is less than or equal to $n$, then 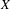$X$ consists entirely of periodic points. However, most proofs of that result use the fact that the number of words of length $n$ in a $\mathbb{Z}$ subshift is non-decreasing in $n$, and we present an example (due to Martin Delacourt) which shows that this monotonicity does not hold for numbers of extender sets (or follower sets) of words of length $n$.