Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T14:01:25.905Z Has data issue: false hasContentIssue false
  • English
  • Français

Commuting rational functions revisited

Part of: Entire and meromorphic functions, and related topics Complex dynamical systems

Published online by Cambridge University Press:  15 August 2019

FEDOR PAKOVICH Open the ORCID record for FEDOR PAKOVICH [Opens in a new window]
FEDOR PAKOVICH*
Affiliation:
Department of Mathematics, Ben Gurion University, P.O. Box 653, Beer Sheva, 8410501, Israel email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 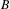$B$ be a rational function of degree at least two that is neither a Lattès map nor conjugate to 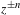$z^{\pm n}$ or 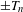$\pm T_{n}$. We provide a method for describing the set 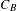$C_{B}$ consisting of all rational functions commuting with 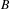$B$. Specifically, we define an equivalence relation 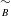$\underset{B}{{\sim}}$ on 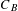$C_{B}$ such that the quotient 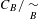$C_{B}/\underset{B}{{\sim}}$ possesses the structure of a finite group 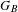$G_{B}$, and describe generators of 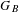$G_{B}$ in terms of the fundamental group of a special graph associated with 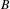$B$.

Keywords

commuting rational functionsthe Ritt theoremcommon iterates

MSC classification

Primary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Secondary: 37F10: Polynomials; rational maps; entire and meromorphic functions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 1 , January 2021 , pp. 295 - 320
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Eremenko, A.. Some functional equations connected with the iteration of rational functions. Leningrad Math. J. 1 (1990), 905–919.Google Scholar
Fatou, P.. Sur l’iteration analytique et les substitutions permutables. J. Math. Pures Appl. (9) 2(1923) 343–384.Google Scholar
Julia, G.. Mémoire sur la permutabilité des fractions rationelles. Ann. Sci. Éc. Norm. Supér (4) 39(3) (1922), 131–215.10.24033/asens.740Google Scholar
Muzychuk, M. and Pakovich, F.. Jordan-Holder theorem for imprimitivity systems and maximal decompositions of rational functions. Proc. Lond. Math. Soc. (3) 102(1) (2011), 1–24.10.1112/plms/pdq009Google Scholar
Pakovich, F.. Finiteness theorems for commuting and semiconjugate rational functions. Preprint, 2015, arXiv:1604:04771.Google Scholar
Pakovich, F.. On semiconjugate rational functions. Geom. Funct. Anal. 26 (2016), 1217–1243.10.1007/s00039-016-0383-6Google Scholar
Pakovich, F.. Polynomial semiconjugacies, decompositions of iterations, and invariant curves. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) XVII (2017), 1417–1446.Google Scholar
Pakovich, F.. Semiconjugate rational functions: a dynamical approach. Arnold Math. J. 4(1) (2018), 59–68.10.1007/s40598-018-0081-6Google Scholar
Pakovich, F.. Recomposing rational functions. Int. Math. Res. Not. IMRN 2019(7) (2019), 1921–1935.10.1093/imrn/rnx172Google Scholar
Pakovich, F.. On generalized Latès maps. J. Anal. Math. accepted.Google Scholar
Ritt, J.. Prime and composite polynomials. Amer. Math. Soc. Transl. Ser. 2 23 (1922), 51–66.10.1090/S0002-9947-1922-1501189-9Google Scholar
Ritt, J. F.. On the iteration of rational functions. Trans. Amer. Math. Soc. 21(3) (1920), 348–356.10.1090/S0002-9947-1920-1501149-6Google Scholar
Ritt, J. F.. Permutable rational functions. Trans. Amer. Math. Soc. 25 (1923), 399–448.10.1090/S0002-9947-1923-1501252-3Google Scholar
Stillwell, J.. Classical Topology and Combinatorial Group Theory (Graduate Texts in Mathematics, 72). Springer, New York, 1993.Google Scholar