Published online by Cambridge University Press: 05 November 2020
Let
 ${\mathbf {G}}$
be a semisimple algebraic group over a number field K,
${\mathbf {G}}$
be a semisimple algebraic group over a number field K,
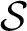 $\mathcal {S}$
a finite set of places of K,
$\mathcal {S}$
a finite set of places of K,
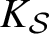 $K_{\mathcal {S}}$
the direct product of the completions
$K_{\mathcal {S}}$
the direct product of the completions
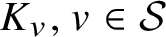 $K_{v}, v \in \mathcal {S}$
, and
$K_{v}, v \in \mathcal {S}$
, and
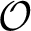 ${\mathcal O}$
the ring of
${\mathcal O}$
the ring of
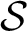 $\mathcal {S}$
-integers of K. Let
$\mathcal {S}$
-integers of K. Let
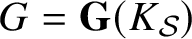 $G = {\mathbf {G}}(K_{\mathcal {S}})$
,
$G = {\mathbf {G}}(K_{\mathcal {S}})$
,
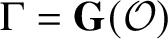 $\Gamma = {\mathbf {G}}({\mathcal O})$
and
$\Gamma = {\mathbf {G}}({\mathcal O})$
and
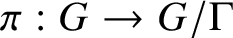 $\pi :G \rightarrow G/\Gamma $
the quotient map. We describe the closures of the locally divergent orbits
$\pi :G \rightarrow G/\Gamma $
the quotient map. We describe the closures of the locally divergent orbits
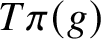 ${T\pi (g)}$
where T is a maximal
${T\pi (g)}$
where T is a maximal
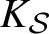 $K_{\mathcal {S}}$
-split torus in G. If
$K_{\mathcal {S}}$
-split torus in G. If
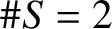 $\# S = 2$
then the closure
$\# S = 2$
then the closure
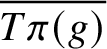 $ \overline{T\pi (g)}$
is a finite union of T-orbits stratified in terms of parabolic subgroups of
$ \overline{T\pi (g)}$
is a finite union of T-orbits stratified in terms of parabolic subgroups of
 ${\mathbf {G}} \times {\mathbf {G}}$
and, consequently,
${\mathbf {G}} \times {\mathbf {G}}$
and, consequently,
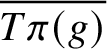 $\overline{T\pi (g)}$
is homogeneous (i.e.
$\overline{T\pi (g)}$
is homogeneous (i.e.
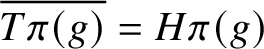 $\overline{T\pi (g)}= H\pi (g)$
for a subgroup H of G) if and only if
$\overline{T\pi (g)}= H\pi (g)$
for a subgroup H of G) if and only if
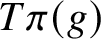 ${T\pi (g)}$
is closed. On the other hand, if
${T\pi (g)}$
is closed. On the other hand, if
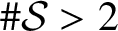 $\# \mathcal {S}> 2$
and K is not a
$\# \mathcal {S}> 2$
and K is not a
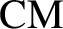 $\mathrm {CM}$
-field then
$\mathrm {CM}$
-field then
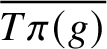 $\overline {T\pi (g)}$
is homogeneous for
$\overline {T\pi (g)}$
is homogeneous for
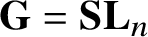 ${\mathbf {G}} = \mathbf {SL}_{n}$
and, generally, non-homogeneous but squeezed between closed orbits of two reductive subgroups of equal semisimple K-ranks for
${\mathbf {G}} = \mathbf {SL}_{n}$
and, generally, non-homogeneous but squeezed between closed orbits of two reductive subgroups of equal semisimple K-ranks for
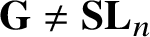 ${\mathbf {G}} \neq \mathbf {SL}_{n}$
. As an application, we prove that
${\mathbf {G}} \neq \mathbf {SL}_{n}$
. As an application, we prove that
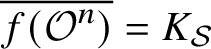 $\overline {f({\mathcal O}^{n})} = K_{\mathcal {S}}$
for the class of non-rational locally K-decomposable homogeneous forms
$\overline {f({\mathcal O}^{n})} = K_{\mathcal {S}}$
for the class of non-rational locally K-decomposable homogeneous forms
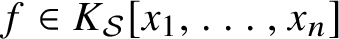 $f \in K_{\mathcal {S}}[x_1, \ldots , x_{n}]$
.
$f \in K_{\mathcal {S}}[x_1, \ldots , x_{n}]$
.