Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-04T22:01:44.522Z Has data issue: false hasContentIssue false
  • English
  • Français

A boundedness theorem for nearby slopes of holonomic 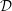${\mathcal{D}}$ -modules

Part of: (Co)homology theory

Published online by Cambridge University Press:  09 September 2016

Jean-Baptiste Teyssier
Jean-Baptiste Teyssier*
Affiliation:
Hebrew University of Jerusalem, Einstein Institute for Mathematics, Givat Ram, Jerusalem, Israel email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using twisted nearby cycles, we define a new notion of slopes for complex holonomic 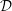${\mathcal{D}}$ -modules. We prove a boundedness result for these slopes, study their functoriality and use them to characterize regularity. For a family of (possibly irregular) algebraic connections 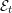${\mathcal{E}}_{t}$ parametrized by a smooth curve, we deduce under natural conditions an explicit bound for the usual slopes of the differential equation satisfied by the family of irregular periods of the 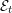${\mathcal{E}}_{t}$ . This generalizes the regularity of the Gauss–Manin connection proved by Griffiths, Katz and Deligne.

Keywords

D-modulenearby cyclesrapid decay homologyirregular periods

MSC classification

Primary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 10 , October 2016 , pp. 2050 - 2070
Copyright
© The Author 2016 

References

Aroca, J.-M., Hironaka, H. and Vicente, J.-L., Desingularization theorems , Mem. Mat. Inst. Jorge Juan 29 (1975).Google Scholar
Bloch, S. and Esnault, H., Homology for irregular connections , J. Theór. Nombres Bordeaux 16 (2004), 357–371.CrossRefGoogle Scholar
Bierstone, E. and Milman, P., Uniformization of analytic spaces , J. Amer. Math. Soc. 2 (1989), 801–836.Google Scholar
Castro, P. and Sabbah, C., Sur les pentes d’un ${\mathcal{D}}$ -module le long d’une hypersurface. Preprint (1989).Google Scholar
Deligne, P., Equations différentielles à points singuliers réguliers, Lecture Notes in Mathematics, vol. 163 (Springer, 1970).Google Scholar
Deligne, P., Lettre à Malgrange. 20 décembre 1983 , in Singularités irrégulières, Documents Mathématiques, vol. 5 (Société Mathématique de France, Paris, 2007), 37–41.Google Scholar
Deligne, P., Letter to V. Drinfeld, June 2011. Detailed account available in: H. Esnault and M. Kerz, A finiteness theorem for Galois representations of function fields over finite fields (after Deligne) , Acta Math. Vietnam 37 (2012), 531–562.Google Scholar
Dimca, A., Maaref, F., Sabbah, C. and Saito, M., Dwork cohomology and algebraic D-modules , Math. Ann. 378 (2000), 107–125.Google Scholar
Griffiths, P. A., Periods of integrals on algebraic manifolds I, II , Amer. J. Math. 90 (1968), 460–495, 496–541.Google Scholar
Grothendieck, A., On the de Rham cohomology of algebraic varieties , Publ. Math. Inst. Hautes Études Sci. 29 (1966), 95–103.Google Scholar
Hien, M., Periods for irregular singular connections on surfaces , Math. Ann. 337 (2007), 631–669.Google Scholar
Hien, M., Periods for flat algebraic connections , Invent. Math. 178 (2009), 1–22.Google Scholar
Hien, M. and Roucairol, C., Integral representations for solutions of exponential Gauss–Manin systems , Bull. Soc. Math. France 136 (2008), 505–532.Google Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., D-Modules, perverse sheaves, and representation theory, Progress in Mathematics, vol. 236 (Birkhäuser, 2000).Google Scholar
Kashiwara, M., On the maximally overdetermined systems of linear differential equations I , Publ. Res. Inst. Math. Sci. 10 (1975), 563–579.Google Scholar
Kashiwara, M., Vanishing cycle sheaves and holonomic systems of differential equations , in Algebraic geometry, Lecture Notes in Mathematics, vol. 1016 (Springer, 1983).Google Scholar
Kashiwara, M. and Kawai, T., On holonomic systems of micro-differential equations , Publ. Res. Inst. Math. Sci. 17 (1981), 813–979.Google Scholar
Katz, N., Nilpotent connections and the monodromy theorem: Applications of a result of Turrittin , Publ. Math. Inst. Hautes Études Sci. 39 (1970), 175–232.Google Scholar
Katz, N. and Oda, T., On the differentiation of De Rham cohomology classes with respect to parameters , J. Math. Kyoto Univ. 8 (1968), 199–213.Google Scholar
Kedlaya, K., Good formal structures for flat meromorphic connections I: Surfaces , Duke Math. J. 154 (2010), 343–418.Google Scholar
Kedlaya, K., Good formal structures for flat meromorpohic connexions II: Excellent schemes , J. Amer. Math. Soc. 24 (2011), 183–229.Google Scholar
Laurent, Y., Polygone de Newton et b-fonctions pour les modules micro-différentiels , Ann. Sci. Éc. Norm. Supér. 20 (1987), 391–441.Google Scholar
Laurent, Y. and Mebkhout, Z., Pentes algébriques et pentes analytiques d’un D-module , Ann. Sci. Éc. Norm. Supér. 32 (1999), 39–69.Google Scholar
Maisonobe, P. and Mebkhout, Z., Le théorème de comparaison pour les cycles évanescents , in Èléments de la théorie des systèmes différentiels géométriques, Cours du C.I.M.P.A., Séminaires et Congrès, vol. 8 (Société Mathématique de France, Paris, 2004), 311–389.Google Scholar
Malgrange, B., Polynômes de Bernstein-Sato et cohomologie évanescente, Astérisque, vols 101–102 (Société Mathématique de France, 1983), 233–267.Google Scholar
Malgrange, B., Connexions méromorphes 2: Le réseau canonique , Invent. Math. 124 (1996), 367–387.Google Scholar
Matsumura, H., Commutative algebra, Mathematics Lecture Note Series, second edition (Benjamin/Cummings, 1980).Google Scholar
Mebkhout, Z., Cohomologie locale des espaces analytiques complexes, PhD thesis, University Paris VII (1979).Google Scholar
Mebkhout, Z., Le théorème de positivité de l’irrégularité pour les D X -modules , in The Grothendieck Festschrift III, Progress in Mathematics, vol. 88 (Birkhäuser, 1990), 83–132.Google Scholar
Mebkhout, Z., Le théorème de positivité, le théorème de comparaison et le théorème d’existence de Riemann , in Èléments de la théorie des systèmes différentiels géométriques, Cours du C.I.M.P.A., Séminaires et Congrès, vol. 8 (Société Mathématique de France, 2004), 165–310.Google Scholar
Mebkhout, Z. and Sabbah, C., Le formalisme des six opérations de Grothendieck pour lesD-modules cohérents, Travaux en cours, vol. 35 (Hermann, Paris, 1989).Google Scholar
Mochizuki, T., Good formal structure for meromorphic flat connections on smooth projective surfaces , in Algebraic analysis and around in honor of Professor Masaki Kashiwara’s 60th birthday (Mathematical Society of Japan, Tokyo, 2009), 223–253.Google Scholar
Mochizuki, T., The Stokes structure of a good meromorphic flat bundle , J. Inst. Math. Jussieu 10 (2011), 675–712.Google Scholar
Mochizuki, T., Wild harmonic bundles and wild pure twistor D-modules, Astérisque, vol. 340 (Société Mathématique de France, 2011).Google Scholar
Sabbah, C., Equations différentielles à points singuliers irréguliers et phénomène de Stokes en dimension 2, Astérisque, vol. 263 (Société Mathématique de France, 2000).Google Scholar
Sabbah, C., Polarizable twistor D-modules, Astérisque, vol. 300 (Société Mathématique de France, 2005), 309–330.Google Scholar
Sabbah, C., An explicit stationary phase formula for the local formal Fourier–Laplace transform , in Singularities, vol. 1, Contemporary Mathematics, vol. 474 (American Mathematical Society, Providence, RI, 2008), 309–330.Google Scholar
Serre, J. P., Géométrie algébrique et géométrie analytique , Ann. Inst. Fourier (Grenoble) 6 (1956), 1–42.Google Scholar
Singer, M. T. and van der Put, M., Galois theory of linear differential equations, Grundlehren der mathematischen Wissenschaften, vol. 328 (Springer, 2000).Google Scholar
Teyssier, J.-B., Nearby slopes and boundedness for $\ell$ -adic sheaves in positive characteristic. Preprint (2015), http://jbteyssier.com/papers/jbteyssier_ladicNearbySlopes.pdf.Google Scholar
Teyssier, J.-B., Vers une catégorie de D-modules holonomes d’irrégularité bornée , in Program for the application to CNRS (2015).Google Scholar
Teyssier, J.-B., Sur une caractérisation des D-modules holonomes réguliers , Math. Res. Lett. 23 (2016), 273–302.Google Scholar
Verdier, J.-L., Spécialisation de faisceaux et monodromie modérée, Astérisque, vols 101–102 (Société Mathématique de France, 1983), 332–364.Google Scholar