Article contents
Rational Points in Arithmetic Progressions on y2 = xn + k
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 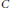 $C$ be a hyperelliptic curve given by the equation
$C$ be a hyperelliptic curve given by the equation 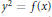 ${{y}^{2}}\,=\,f(x)$ for
${{y}^{2}}\,=\,f(x)$ for 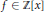 $f\,\in \,\mathbb{Z}[x]$ without multiple roots. We say that points
$f\,\in \,\mathbb{Z}[x]$ without multiple roots. We say that points 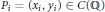 ${{P}_{i}}\,=\,({{x}_{i}},\,{{y}_{i}})\,\in \,C(\mathbb{Q})$ for
${{P}_{i}}\,=\,({{x}_{i}},\,{{y}_{i}})\,\in \,C(\mathbb{Q})$ for 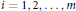 $i\,=\,1,\,2,\,\ldots ,\,m$ are in arithmetic progression if the numbers
$i\,=\,1,\,2,\,\ldots ,\,m$ are in arithmetic progression if the numbers  ${{x}_{i}}$ for
${{x}_{i}}$ for 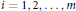 $i\,=\,1,\,2,\,\ldots ,\,m$ are in arithmetic progression.
$i\,=\,1,\,2,\,\ldots ,\,m$ are in arithmetic progression.
In this paper we show that there exists a polynomial 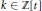 $k\,\in \,\mathbb{Z}[t]$ with the property that on the elliptic curve
$k\,\in \,\mathbb{Z}[t]$ with the property that on the elliptic curve 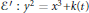 $\varepsilon \prime :{{y}^{2}}={{x}^{3}}+k(t)$ (defined over the field
$\varepsilon \prime :{{y}^{2}}={{x}^{3}}+k(t)$ (defined over the field 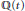 $\mathbb{Q}(t)$) we can find four points in arithmetic progression that are independent in the group of all
$\mathbb{Q}(t)$) we can find four points in arithmetic progression that are independent in the group of all 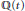 $\mathbb{Q}(t)$-rational points on the curve
$\mathbb{Q}(t)$-rational points on the curve 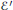 $\varepsilon \prime $. In particular this result generalizes earlier results of Lee and Vélez. We also show that if
$\varepsilon \prime $. In particular this result generalizes earlier results of Lee and Vélez. We also show that if 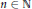 $n\,\in \,\mathbb{N}$ is odd, then there are infinitely many
$n\,\in \,\mathbb{N}$ is odd, then there are infinitely many  $k$'s with the property that on curves
$k$'s with the property that on curves  ${{y}^{2}}\,=\,{{x}^{n}}\,+\,k$ there are four rational points in arithmetic progressions. In the case when
${{y}^{2}}\,=\,{{x}^{n}}\,+\,k$ there are four rational points in arithmetic progressions. In the case when  $n$ is even we can find infinitely many
$n$ is even we can find infinitely many  $k$'s such that on curves
$k$'s such that on curves  ${{y}^{2}}\,=\,{{x}^{n}}\,+\,k$ there are six rational points in arithmetic progression.
${{y}^{2}}\,=\,{{x}^{n}}\,+\,k$ there are six rational points in arithmetic progression.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
- 6
- Cited by


