Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T22:20:13.733Z Has data issue: false hasContentIssue false
  • English
  • Français

The Associative Part of a Convergence Domain is Invariant

Published online by Cambridge University Press:  20 November 2018

John J. Sember
John J. Sember*
Affiliation:
Simon Fraser University, Burnaby, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Of special interest in summability theory are those conservative matrices possessing the "mean-value property". If cA={x: Ax ∊ c} denotes the convergence domain of a conservative matrix A, then A has the mean-value property in case, for each x in cA, there exists M = M(A, x) > 0 such that

1

This property has been considered by many writers and has been shown, among other things, to be equivalent to the requirement that the matrix be associative, i.e., for each x in cA

2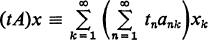

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 1 , March 1970 , pp. 147 - 148
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Wilansky, A., Distinguished subsets and summability invariants, J. Analys. Math. 12 (1964), 327-350.Google Scholar