Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T16:21:11.230Z Has data issue: false hasContentIssue false
  • English
  • Français

Value Sets of Sparse Polynomials

Part of: Finite fields and commutative rings (number-theoretic aspects) Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  24 September 2019

Igor E. Shparlinski  and
José Felipe Voloch
Igor E. Shparlinski
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney NSW 2052, Australia Email: [email protected]
José Felipe Voloch
Affiliation:
School of Mathematics and Statistics, University of Canterbury, Private Bag 4800, Christchurch 8140, New Zealand Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain a new lower bound on the size of the value set 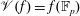$\mathscr{V}(f)=f(\mathbb{F}_{p})$ of a sparse polynomial 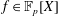$f\in \mathbb{F}_{p}[X]$ over a finite field of 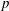$p$ elements when 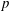$p$ is prime. This bound is uniform with respect to the degree and depends on some natural arithmetic properties of the degrees of the monomial terms of 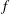$f$ and the number of these terms. Our result is stronger than those that can be extracted from the bounds on multiplicities of individual values in 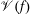$\mathscr{V}(f)$.

Keywords

sparse polynomialvalue setrational point on curve

MSC classification

Primary: 11T06: Polynomials
Secondary: 14G15: Finite ground fields
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 187 - 196
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author I. E. S. was supported by ARC Grants DP170100786 and DP180100201.

References

Bi, J., Cheng, Q., and Rojas, J. M., Sub-linear root detection, and new hardness results, for sparse polynomials over finite fields. SIAM J. Comput. 45(2016), 1433–1447. https://doi.org/10.1137/140990401Google Scholar
Birch, B. J. and Swinnerton-Dyer, H. P. F., Note on a problem of Chowla. Acta Arith. 5(1959), 417–423. https://doi.org/10.4064/aa-5-4-417-423Google Scholar
Canetti, R., Friedlander, J. B., Konyagin, S. V., Larsen, M., Lieman, D., and Shparlinski, I. E., On the statistical properties of Diffie-Hellman distributions. Israel J. Math. 120(2000), 23–46. https://doi.org/10.1007/s11856-000-1270-1Google Scholar
Carlitz, L., Lewis, D. J., Mills, W. H., and Strauss, E. G., Polynomials over finite fields with minimal value sets. Mathematika 8(1961), 121–130. https://doi.org/10.1112/S0025579300002230Google Scholar
Cheng, Q., Gao, S., Rojas, J. M., and Wan, D., Sparse univariate polynomials with many roots over finite fields. Finite Fields Appl. 46(2017), 235–246. https://doi.org/10.1016/j.ffa.2017.03.006Google Scholar
Kelley, A., Roots of sparse polynomials over a finite field. LMS J. Comput. Math. 19(2016), suppl. A, 196–204. https://doi.org/10.1112/S1461157016000334Google Scholar
Kurlberg, P., Poisson spacing statistics for value sets of polynomials. Int. J. Number Theory 5(2009), 489–513. https://doi.org/10.1142/S1793042109002237Google Scholar
Lorenzini, D., An invitation to arithmetic geometry. Graduate Studies in Mathematics, 9, American Mathematical Society, Providence, RI, 1996. https://doi.org/10.1090/gsm/009Google Scholar
Mills, W. H., Polynomials with minimal value sets. Pacific J. Math. 14(1964), 225–241.Google Scholar
Mullen, G. and Zieve, M., Value sets of polynomials. In: Handbook of finite fields. CRC Press, Boca Raton, FL, 2013, pp. 232–235. https://doi.org/10.1201/b15006Google Scholar
Stichtenoth, H., Algebraic function fields and codes. Graduate Texts in Mathematics, 254, Springer-Verlag, Berlin, 2009.Google Scholar
Stöhr, K. O. and Voloch, J. F., Weierstrass points and curves over finite fields. Proc. London Math. Soc. 52(1986), 1–19. https://doi.org/10.1112/plms/s3-52.1.1Google Scholar
Voloch, J. F., Diagonal equations over function fields. Bol. Soc. Brasil. Mat. 16(1985), 29–39. https://doi.org/10.1007/BF02584799Google Scholar
Voloch, J. F., On the number of values taken by a polynomial over a finite field. Acta Arith. 52(1989), 197–201. https://doi.org/10.4064/aa-52-2-197-201Google Scholar
Wan, D., Shiue, P. J.-S., and Chen, C. S., Value sets of polynomials over finite fields. Proc. Amer. Math. Soc. 119(1993), 711–717. https://doi.org/10.2307/2160504Google Scholar
Zannier, U., On the number of terms of a composite polynomial. Acta Arith. 127(2007), 157–168. https://doi.org/10.4064/aa127-2-5Google Scholar