Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T14:33:50.789Z Has data issue: false hasContentIssue false
  • English
  • Français

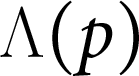A Non-abelian, Non-Sidon, Completely Bounded $\Lambda (p)$ Set

Part of: Harmonic analysis in one variable Abstract harmonic analysis

Published online by Cambridge University Press:  26 February 2020

Kathryn E. Hare  and
Parasar Mohanty
Kathryn E. Hare*
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada
Parasar Mohanty
Affiliation:
Department of Mathematics and Statistics, Indian Institute of Technology, Kanpur, India, 208016 e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of this note is to construct an example of a discrete non-abelian group G and a subset E of G, not contained in any abelian subgroup, that is a completely bounded 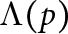$\Lambda (p)$ set for all 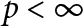$p<\infty ,$ but is neither a Leinert set nor a weak Sidon set.

Keywords

Completely boundedSidon setnon-amenable group

MSC classification

Primary: 43A46: Special sets (thin sets, Kronecker sets, Helson sets, Ditkin sets, Sidon sets, etc.) 43A30: Fourier and Fourier-Stieltjes transforms on nonabelian groups and on semigroups, etc.
Secondary: 42A55: Lacunary series of trigonometric and other functions; Riesz products
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 1 , March 2021 , pp. 1 - 7
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bożejko, M., The existence of $\varLambda (p)$sets in discrete non-commutative groups. Boll. Un. Mat. Ital. 8(1973), 579–582.Google Scholar
Bożejko, M., A remark to my paper: “The existence of $\varLambda (p)$sets in discrete noncommutative groups” (Boll. Un. Mat. Ital. 8(1973), 579–582). Boll. Un. Mat. Ital. 11(1975), 43.Google Scholar
Eymard, P., L’algèbre de Fourier d’un groupe localement compact. Bull. Soc. Math. France 92(1964), 181–236.Google Scholar
Figà-Talamanca, A. and Picardello, M., Multiplicateurs de $A(G)$qui ne sont pas dans $B(G)$. C. R. Acad. Sci. Paris Sér. A-B 277(1973), A117–A119.Google Scholar
Graham, C. and Hare, K., Interpolation and Sidon sets in compact groups. CMS Books in Mathematics, Springer, New York, 2013. https://doi.org/10.1007/9781-4614-5392-5Google Scholar
Harcharras, A., Fourier analysis, Schur multipliers on ${S}^p$and non-commutative $\varLambda (p)$sets. Studia Math. 137(1999), 203–260. https://doi.org/10.4064/sm-137-3-203-260CrossRefGoogle Scholar
Hare, K. E. and Mohanty, P., Completely bounded $\varLambda (p)$sets that are not Sidon. Proc. Amer. Math. Soc. 144(2016), 2861–2869. https://doi.org/10.1090/proc/13039CrossRefGoogle Scholar
Leinert, M., Faltungsoperatoren auf gewissen diskreten Gruppen. Studia Math. 52(1974), 149–158. https://doi.org/10.4064/sm-52-2-149-158Google Scholar
López, J. and Ross, K., Sidon sets. Lecture Notes in Pure and Applied Mathematics, 13, Marcel Dekker, Inc., New York, 1975.Google Scholar
Picardello, M., Lacunary sets in discrete noncommutative groups. Boll. Un. Mat. Ital. 8(1973), 494–508.Google Scholar
Pisier, G., The operator Hilbert space $\mathrm{OH}$, complex interpolation and tensor norms. Mem. Amer. Math. Soc. 122(1996), no. 585. https://doi.org/10.1090/memo/0585CrossRefGoogle Scholar
Pisier, G. and Xu, Q., Non-commutative ${L}^p$-spaces. Handbook of the geometry of Banach spaces, 2, North-Holland, Amsterdam, 2003, pp. 1459–1517. https://doi.org/10.1016/S1874-5849(03)80041-4CrossRefGoogle Scholar
Pisier, G., Multipliers and lacunary sets in non-amenable groups. Amer. J. Math. 117(1995), 337–376. https://doi.org/10.2307/2374918CrossRefGoogle Scholar
Popa, A.-M., On completely bounded multipliers of the Fourier algebra $A(G)$. Ph. D. thesis, University of Illinois at Urbana-Champaign. 2008.Google Scholar
Rudin, W., Trigonometric series with gaps. J. Math. Mech. 9(1960), 203–227. https://doi.org/10.1512/iumj.1960.9.59013CrossRefGoogle Scholar
Wang, S., Lacunary Fourier series for compact quantum groups. Comm. Math. Phys. 349(2017), 895–945. https://doi.org/10.1007/s00220-016-2670-3CrossRefGoogle Scholar