Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T16:28:39.411Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypersurfaces with Prescribed Boundary and Small Steklov Eigenvalues

Part of: Spectral theory and eigenvalue problems Calculus on manifolds; nonlinear operators

Published online by Cambridge University Press:  12 December 2019

Bruno Colbois ,
Alexandre Girouard  and
Antoine Métras
Bruno Colbois
Affiliation:
Université de Neuchâtel, Institut de Mathématiques, Rue Emile-Argand 11, CH-2000 Neuchâtel, Switzerland Email: [email protected]
Alexandre Girouard
Affiliation:
Département de mathématiques et de statistique, Université Laval, Pavillon AlexandreVachon, 1045, av. de la Médecine, Québec Qc G1V 0A6, Canada Email: [email protected]
Antoine Métras
Affiliation:
Département de mathématiques et de statistique, Université de Montréal, CP 6128 succ Centre-Ville, Montréal, QC H3C 3J7, Canada Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a smooth compact hypersurface 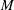$M$ with boundary 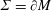$\unicode[STIX]{x1D6F4}=\unicode[STIX]{x2202}M$, we prove the existence of a sequence 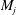$M_{j}$ of hypersurfaces with the same boundary as 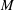$M$, such that each Steklov eigenvalue 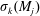$\unicode[STIX]{x1D70E}_{k}(M_{j})$ tends to zero as 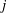$j$ tends to infinity. The hypersurfaces 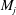$M_{j}$ are obtained from 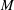$M$ by a local perturbation near a point of its boundary. Their volumes and diameters are arbitrarily close to those of 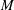$M$, while the principal curvatures of the boundary remain unchanged.

Keywords

Steklov eigenvaluehypersurface

MSC classification

Primary: 35P15: Estimation of eigenvalues, upper and lower bounds
Secondary: 58C40: Spectral theory; eigenvalue problems
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 46 - 57
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chavel, I., Eigenvalues in Riemannian geometry. Pure and Applied Mathematics, 115, Academic Press, Inc., Orlando, FL, 1984.Google Scholar
Cianci, D. and Girouard, A., Large spectral gaps for Steklov eigenvalues under volume constraints and under localized conformal deformations. Ann. Global Anal. Geom. 54(2018), 529–539. https://doi.org/10.1007/s10455-018-9612-6CrossRefGoogle Scholar
Colbois, B., The spectrum of the Laplacian: a geometric approach. In: Geometric and computational spectral theory. Contemp. Math., 700, American Mathematical Society, Providence, RI, 2017, pp. 1–40. https://doi.org/10.1090/conm/700/14181Google Scholar
Colbois, B., El Soufi, A., and Girouard, A., Compact manifolds with fixed boundary and large Steklov eigenvalues. Proc. Amer. Math. Soc. 147(2019), 3813–3827. https://doi.org/10.1090/proc/14426CrossRefGoogle Scholar
Colbois, B., Girouard, A., and Gittins, K., Steklov eigenvalues of submanifolds with prescribed boundary in Euclidean space. J. Geom. Anal. 29(2019), 1811–1834. https://doi.org/10.1007/s12220-018-0063-xCrossRefGoogle Scholar
Colbois, B., Girouard, A., and Hassennezhad, A., The Steklov and Laplacian spectra of Riemannian manifolds with boundary. J. Funct. Anal. To appear. https://doi.org/10.1016/j.jfa.2019.108409Google Scholar
Girouard, A., Parnovski, L., Polterovich, I., and Sher, D. A., The Steklov spectrum of surfaces: asymptotics and invariants. Math. Proc. Cambridge Philos. Soc. 157(2014), 379–389. https://doi.org/10.1017/S030500411400036XCrossRefGoogle Scholar
Girouard, A. and Polterovich, I., On the Hersch–Payne–Schiffer inequalities for Steklov eigenvalues. Functional Analysis and its Applications 44(2010), 106–117.CrossRefGoogle Scholar
Girouard, A. and Polterovich, I., Spectral geometry of the Steklov problem. J. Spectr. Theory 7(2017), 321–359. https://doi.org/10.4171/JST/164CrossRefGoogle Scholar
Hirsch, M. W., Differential topology. Graduate Texts in Mathematics, 33, Springer-Verlag, New York-Heidelberg, 1976.CrossRefGoogle Scholar
Karpukhin, M., Bounds between Laplace and Steklov eigenvalues on nonnegatively curved manifolds. Electron. Res. Announc. Math. Sci. 24(2017), 100–109. https://doi.org/10.3934/era.2017.24.011Google Scholar
Kuznetsov, N., Kulczycki, T., Kwaśnicki, M., Nazarov, A., Poborchi, S., Polterovich, I., and Siudeja, B., The legacy of Vladimir Andreevich Steklov. Notices Amer. Math. Soc. 61(2014), 9–22. https://doi.org/10.1090/noti1073CrossRefGoogle Scholar
Lee, J. M. and Uhlmann, G., Determining anisotropic real-analytic conductivities by boundary measurements. Comm. Pure Appl. Math. 42(1989), 1097–1112. https://doi.org/10.1002/cpa.3160420804CrossRefGoogle Scholar
Provenzano, L. and Stubbe, J., Weyl-type bounds for Steklov eigenvalues. J. Spectr. Theory 9(2019), 349–377. https://doi.org/10.4171/JST/250CrossRefGoogle Scholar
Shamma, S. E., Asymptotic behavior of Stekloff eigenvalues and eigenfunctions. SIAM J. Appl. Math. 20(1971), 482–490. https://doi.org/10.1137/0120050CrossRefGoogle Scholar
Wang, Q. and Xia, C., Sharp bounds for the first non-zero Stekloff eigenvalues. J. Funct. Anal. 257(2009), 2635–2644. https://doi.org/10.1016/j.jfa.2009.06.008CrossRefGoogle Scholar