Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T06:05:46.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Trace Forms on Lie Algebras

Published online by Cambridge University Press:  20 November 2018

Richard Block
Richard Block*
Affiliation:
California Institute of Technology
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If L is a Lie algebra with a representation Δ a→aΔ (a in L) (of finite degree), then by the trace form f = fΔ of Δ is meant the symmetric bilinear form on L obtained by taking the trace of the matrix products:

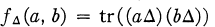
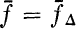Then f is invariant, that is, f is symmetric and f(ab, c) — f(a, bc) for all a, b, c in L. By the Δ-radical L⊥ = L⊥ of L is meant the set of a in L such that f(a, b) = 0 for all b in L. Then L⊥ is an ideal and f induces a bilinear form , called a quotient trace form, on L/L⊥. Thus an algebra 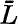has a quotient trace form if and only if there exists a Lie algebra L with a representation Δ such that

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 553 - 564
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Albert, A. A. and Frank, M. S., Simple Lie algebras of characteristic p, Univ. e Politec. Torino Rend. Sem. Mat., 14 (1954-55), 117–139.Google Scholar
2. Block, R., New simple Lie algebras of prime characteristic, Trans. Amer. Math. Soc, 89 (1958), 421–449.Google Scholar
3. Block, R., On Lie algebras of classical type, Proc. Amer. Math. Soc, 11 (1960), 377–379.Google Scholar
4. Cartier, P. et al., Théorie des algebres de Lie, Topologie des groupes de Lie, Séminaire “Sophus Lie,” Ecole Normale Supérieure, Ie année: 1954/55 (Paris, 1955).Google Scholar
5. Curtis, C. W., Modular Lie algebras II, Trans. Amer. Math. Soc, 86 (1957), 91–108.Google Scholar
6. Curtis, C. W., Representations of Lie algebras of classical type with applications to linear groups, J. Math. Mech., 9 (1960), 307–326.Google Scholar
7. Jacobson, N., Classes of restricted Lie algebras of characteristic p. I, Amer. J. Math., 63 (1941), 481–515.Google Scholar
8. Kaplansky, I., Lie algebras of characteristic p, Trans. Amer. Math. Soc, 89 (1958), 149–183.Google Scholar
9. Mills, W. H., Classical type Lie algebras of characteristic 5 and 7, J. Math. Mech., 6 (1957), 559–566.Google Scholar
10. Mills, W. H. and Seligman, G. B., Lie algebras of classical type, J. Math. Mech., 6 (1957), 519–548.Google Scholar
11. Seligman, G. B., On Lie algebras of prime characteristic, Mem. Amer. Math. Soc, 19 (1956).Google Scholar
12. Seligman, G. B., Some remarks on classical Lie algebras, J. Math. Mech., 6 (1957), 549–558.Google Scholar
13. Zassenhaus, H., Ueber Lie ‘sche Ringe mit Primzahlcharakteristik, Abh. Math. Sem. Univ. Hamburg, 13 (1939), 1–100.Google Scholar
14. Zassenhaus, H., Lie-rings and Lie-algebras, Canadian Math. Congress, Summer Seminar, 1957. Ninth Lecture.Google Scholar
15. Zassenhaus, H., On trace bilinear forms on Lie algebras, Proc. Glasgow Math. Assoc, 4 (1959), 62–72.Google Scholar