Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T12:42:39.932Z Has data issue: false hasContentIssue false
  • English
  • Français

A Theorem on k-Saturated Graphs

Published online by Cambridge University Press:  20 November 2018

A. Hajnal
A. Hajnal*
Affiliation:
University of California, Berkeley
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

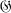In this paper we consider finite graphs without loops and multiple edges. A graph is considered to be an ordered pair 〈G, 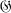*〉 where G is a finite set the elements of which are called the vertices of 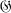while 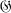* is a subset of [G]2 (where [G]2 is the set of all subsets of two elements of G). The elements of 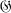* are called the edges of 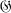. If {P, Q} ∊ 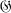*, we say that Q is adjacent to P. The degree of a vertex is the number of vertices adjacent to it. Let k be an integer. We say that 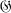is the complete k-graph if G has k elements and * = [G]2.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 17 , 1965 , pp. 720 - 724
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Erd, P.ös and T. Gallai, On the minimal number of vertices representing the edges of a graph, Hung. Acad. Sci., 6 (1961), 181–203.Google Scholar
2. Erd, P.ös, Hajnal, A., and Moon, J. W., A problem in graph theory, Amer. Math. Monthly, to appear.Google Scholar
3. Erdös, P. and Rényi, A., Egy gráfelméleti problémárol, Publ. Math. Inst. Hung. Acad. Sci., 7B (1962), 623–641.Google Scholar
4. Ore, O., Graphs and matching theorems, Duke Math. J., 22 (1955), 615–639.Google Scholar
5. Zykov, A. A., On some properties of linear complexes (Mat. Sb., N.S., 24 (66) (1949), 163–188 (in Russian).Google Scholar