Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:12:51.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly Projective Graphs

Published online by Cambridge University Press:  20 November 2018

Benoit Larose
Benoit Larose*
Affiliation:
Department of Mathematics, Champlain Regional College, 900 Riverside St-Lambert, Quebec, J4P 3P2 Department of Mathematics and Statistics, Concordia University, 1455 de Maisonneuve West Montréal, Quebec, H3G 1M8, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce the notion of strongly projective graph, and characterise these graphs in terms of their neighbourhood poset. We describe certain exponential graphs associated to complete graphs and odd cycles. We extend and generalise a result of Greenwell and Lovász [6]: if a connected graph 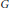$G$ does not admit a homomorphism to $K$, where $K$ is an odd cycle or a complete graph on at least 3 vertices, then the graph 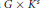$G\,\times \,{{K}^{S}}$ admits, up to automorphisms of $K$, exactly $s$ homomorphisms to $K$.

Keywords

05C1506A99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 4 , 01 August 2002 , pp. 757 - 768
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Corominas, E., Sur les ensembles ordonnés projectifs et la propriété du point fixe. C. R. Acad. Sci. Paris Sér. I Math. 311 (1990), 199–204.Google Scholar
[2] Davey, B. A., Nation, J. B., McKenzie, R. N. and Pálfy, P. P., Braids and their monotone clones. Algebra Universalis (2) 32 (1994), 153–176.Google Scholar
[3] Demetrovics, J. and R´onyai, L., Algebraic properties of crowns and fences. Order 6 (1989), 91–100.Google Scholar
[4] Duffus, D., Sands, B. and Woodrow, R. E., On the chromatic number of the product of graphs. J. Graph Theory 9 (1985), 487–495.Google Scholar
[5] El-Zahar, M. and Sauer, N., The chromatic number of the product of two 4-chromatic graphs is 4. Combinatorica 5 (1985), 121–126.Google Scholar
[6] Greenwell, D. and Lovász, L., Applications of product colourings. Acta Math. Acad. Sci. Hungar. 25 (1974), 335–340.Google Scholar
[7] Hahn, G. and Tardif, C., Graph homomorphisms: structure and symmetry. In: Graph Symmetry, Algebraic Methods and Applications, (eds., G. Hahn and G. Sabidussi), NATO ASI Ser. C 497, Kluwer Academic Publishers, Dordrecht, 1997, 107–166.Google Scholar
[8] Hazan, S., Two properties of projective orders Order 9 (1992), 233–238.Google Scholar
[9] Hedetniemi, S. H., Homomorphisms of graphs and automata. University of Michigan Technical Report 03105-44-T, 1966.Google Scholar
[10] Larose, B., A property of projective ordered sets. European J. Combin. 13 (1992), 371–378.Google Scholar
[11] Larose, B., Families of strongly projective graphs. Discuss. Math. Graph Theory, to appear.Google Scholar
[12] Larose, B., Opérations isotones: crit`ere de complétude. propriétés du point fixe et de projection, Ph.D. thesis, Université de Montréal, (1993), 128 pages.Google Scholar
[13] Larose, B. and Tardif, C., Projectivity and independent sets in powers of graphs. J. Graph Theory, to appear.Google Scholar
[14] Larose, B. and Tardif, C., Strongly rigid graphs and projectivity. Mult. Val. Logic, to appear.Google Scholar
[15] Larose, B. and Tardif, C., Hedetniemi's conjecture and the retracts of products of graphs. Combinatorica (4) 20 (2000), 531–544.Google Scholar
[16] Larose, B. and Zádori, L., Algebraic properties and dismantlability of finite posets. Discrete Math. 163 (1997), 89–99.Google Scholar
[17] Lovász, L., Operations with structures. Acta Math. Acad. Sci. Hungar. 18 (1967), 321–328.Google Scholar
[18] Nešetřil, J. and Zhu, X., On sparse graphs with given colorings and homomorphisms. preprint, 13 pages, 2000.Google Scholar