Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T16:16:59.171Z Has data issue: false hasContentIssue false
  • English
  • Français

Orthogonal Decompositions of Multivariate Weakly Stationary Stochastic Processes

Published online by Cambridge University Press:  20 November 2018

James B. Robertson
James B. Robertson*
Affiliation:
Cornell University, Ithaca, N. Y.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall study the relations between the ranks of g-variate, discrete-parameter, weakly stationary stochastic processes x, y, and z satisfying the condition

1.1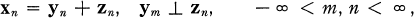

and derive from them a characterization for the Wold decomposition and conditions for the concordance of the Wold and the Lebesgue-Cramér decompositions.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 368 - 383
Copyright
Copyright © Canadian Mathematical Society 1968

Footnotes

1

Vectors and subspaces of Xq and q X q matrices will be written in boldface, while vectors and subspaces in X will not be written in boldface.

References

1. Cramer, H., On the theory of stationary random processes, Ann. of Math., 18 (1940), 215–230.Google Scholar
2. Gladyshev, E., On multi-dimensional stationary stochastic processes, Theor. Probability Appl. 3 (1958), 425–428.Google Scholar
3. Halmos, P., Finite dimensional vector spaces (London, 1942).Google Scholar
3a. Halmos, P. Shifts on Hilbert space, J. Reine Angew. Math., 208 (1961), 102–112.Google Scholar
4. Kolmogorov, A., Stationary sequences in Hilbert space (Russian), Bull. Math. Univ. Moscow, 2 (1941) (translation by N. Artin).Google Scholar
5. Masani, P., Cramer's theorem on monotone matrix-valued functions and the Wold decomposition, Prob. and Stat., The Harald Cramer Volume (New York, 1959), pp. 175–189.Google Scholar
6. Masani, P., Shift invariant spac 's and prediction theory, Acta Math., 107 (1962), 275–290.Google Scholar
7. Masani, P., Isometric flows on Hilbert space, Bull. Amer Math. Soc, 68 (1962), 624–632.Google Scholar
8. Masani, P. and Robertson, J., The time domain analysis of a continuous parameter weakly stationary stochastic process, Pacific J. Math., 12 (1962), 1361–1378.Google Scholar
9. Robertson, J., On wandering sub spaces for unitary operators, Proc. Amer. Math. Soc, 16 1965), 233–236.Google Scholar
10. Rosenberg, M., The sguar e-integr ability of matrix-valued functions with respect to a nonnegative hermitian measure, Duke Math. J., 81 (1964), 291–298.Google Scholar
11. Rosenberg, M., Spectral analysis of multivariate weakly stationary stochastic processes (Doctoral dissertation, Indiana University, 1964).Google Scholar
12. Rozanov, Yu, Linear extrapolation of multi-dimensional stationary processes of rank one with discrete time, Dokl. Akad. Nauk SSSR, 125 (1959), 277–280.Google Scholar
13. Wiener, N. and Masani, P., The prediction theory of multivariate stochastic processes, Acta Math., 98 (1957), 111–150.Google Scholar
14. Ze-pei, Jang, The prediction theory of multivariate stationary processes, I and II, Chinese Math., 4 (1963), 291-322 ; 5 (1963), 471–484.Google Scholar