Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T09:34:22.965Z Has data issue: false hasContentIssue false
  • English
  • Français

On Implicational Completeness

Published online by Cambridge University Press:  20 November 2018

Shafaat Ahmad
Shafaat Ahmad*
Affiliation:
Université Laval, Quebéc, Quebéc
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A class 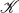of (universal) algebras [4; 5] of the same type or species τ is called equationally complete if the variety [4] Var(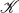) generated by 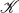has exactly two subvarieties —namely Var(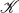) itself and the class of all one element algebras. I t follows that equationally complete varieties are the atoms in the complete lattice of all varieties of a given type of algebras. J. Kalicki, D. Scott [7; 8; 9; 10] and others [2; 3; 6; 12] have considered several questions about equational completeness. A good many of these results have appeared in books. (See, for instance, [4, 5], to which we also refer the reader for more extensive bibliography on subjects related to equational completeness.)

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 3 , June 1974 , pp. 761 - 768
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Ahmad, Shafaat, Subcartesian products of finitely many finite algebras, Proc. Amer. Math. Soc. 26 (1970), 401–404.Google Scholar
2. Bol'bot, A. D., O mnogoobrazÿach Ω-algebr, Algebra i Logika 9 (1970), 406–414.Google Scholar
3. Burris, S., On the structure of the lattice of equational classes, L(τ), Algebra Universalis 1 (1971), 39–45.Google Scholar
4. Cohn, P. M., Universal Algebra (Harper and Row, New York, 1965).Google Scholar
5. Gratzer, G., Universal Algebra (Van Nostrand, New York, 1968).Google Scholar
6. Jezk, J., On atoms in the lattice of primitive classes, Comment. Math. Univ. Carolinae 11 (1970), 515–532.Google Scholar
7. Kalicki, J., The number of equationally complete classes of equations, Nederl. Akad. Wetensch. Proc. Ser. A 58 (1955), 660–662.Google Scholar
8. Kalicki, J. and Scott, D., Some equationally complete algebras, Bull. Amer. Math. Soc. 59 (1953), 77–78.Google Scholar
9. Kalicki, J. and Scott, D., Equational completeness and abstract algebras, Nederl. Akad. Wetensch. Proc. Ser. A 58 (1955), 650–659.Google Scholar
10. Scott, D., Equationally complete extensions of finite algebras, Nederl. Akad. Wetensch. Proc. Ser. A 59 (1956), 35–38.Google Scholar
11. Tarski, A., Fundamentale Begriffe der Méthodologie der deduktiven Wissenschaften. I, Monatsh. Mat. 37 (1930), 361–404.Google Scholar
12. Tarski, A., Equationally complete rings and relation algebras, Indag. Math. 18 (1956), 39–46.Google Scholar
13. Tarski, A., Logic, semantics, and metamaihematics (Oxford at the Clarendon Press, 1956).Google Scholar