Any real number y leads to a continued fraction of the type

(1)

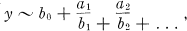
where ai, bi are integers which satisfy the inequalities

(2)

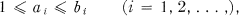
by means of the algorithm

(3)

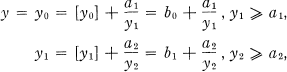
the a's being assigned positive integers. The process terminates for rational y; the last denominator bk satisfying bk ≥ ak + 1. For irrational y, the process does not terminate. For a preassigned set of numerators ai ≥ 1, this C.F. development of y is unique; its value being y.

Bankier and Leighton (1) call such fractions (1), which satisfy (2), proper continued fractions. Among other questions, they studied the problem of expanding quadratic surds in periodic continued fractions. They state that “it is well-known that not only does every periodic regular continued fraction represent a quadratic irrational, but the regular continued fraction expansion of a quadratic irrational is periodic.