Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stevens, Harlan
and
Kuty, Larry
1968.
Applications of an elementary theorem to number theory.
Archiv der Mathematik,
Vol. 19,
Issue. 1,
p.
37.


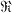 of q elements, let {
of q elements, let {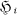 } be a collection of s subsets of
} be a collection of s subsets of 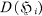 denote the set of all differences d′ — d″ with d′ and d″ from
denote the set of all differences d′ — d″ with d′ and d″ from