Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T12:03:26.993Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattices With a Given Abstract Group of Automorphisms

Published online by Cambridge University Press:  20 November 2018

Robert Frucht
Robert Frucht*
Affiliation:
Technical University Santa Maria, Valparaiso (Chile)
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem of finding a lattice with a given abstract group of automorphisms has been solved by Garrett Birkhoff who proved that for any group of order g there exists a distributive lattice with at most 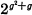elements. That this number can be somewhat reduced by modifications of Birkhoff's original procedure has already been shown by the author; it turns out, however, that it remains rather high for finite groups of relatively low order.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 2 , 1950 , pp. 417 - 419
Copyright
Copyright © Canadian Mathematical Society 1950

References

1 For the definition of lattice and other basic notions of lattice theory, see Garrett Birkhoff's Lattice Theory (1st ed., New York, 1940).

2 Birkhoff, Garrett, Sobre los grupos de automorfismos. Revista de la Union Matematica Argentina, vol. 11 (1946), pp. 155–157.Google Scholar

3 Frucht, R., Sobre la construction de sistemas parcialmente ordenados con grupo de automorfismos dado. Revista de la Union Matematica Argentina, vol. 13 (1948), pp. 12–18. See also: On the construction of partially ordered systems with a given group of automorphisms. Amer. J. Math., vol. 72 (1950), pp. 195–199.Google Scholar

4 In other words, S is the “cell-space” P(G) of G (see Lattice Theory, 1st ed., p. 15) to which an 0 has been added in order to obtain a lattice.

5 The “Hasse diagram” of this lattice may be obtained from the right-hand half of Fig 2 p. 15, of Lattice Theory by adding an 0 and joining it with B1, B2, B3 and B4.

6 Lattice Theory, 1st ed., p. 34, Corollary 3 to Theorem 3.1.

7 By “X covers A” it is meant that X > A, while no Z of 5 satisfies X > Z > A.

8 Frucht, R., Graphs of degree 3 with a given abstract group. Can. J. Math., vol. 1 (1949), pp. 365–378.CrossRefGoogle Scholar