Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-20T14:36:16.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Inversion Theorems for the Laplace-Stieltjes Transform

Published online by Cambridge University Press:  20 November 2018

Z. Ditzian  and
A. Jakimovski
Z. Ditzian
Affiliation:
The Hebrew University and Tel-Aviv University
A. Jakimovski
Affiliation:
The Hebrew University and Tel-Aviv University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Laplace-Stieltjes transform f(x) of the function α(t) is denned by

1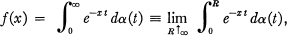

where α(t) is a function of bounded variation in each closed interval [0, R] (R > 0) and the right-hand side of (1) is supposed to be convergent for some x = X0. The Laplace transform f(x) of the function ϕ(t) is defined by

2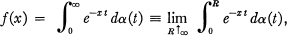

where ϕ(t) ∈ L1(0, R) for each R > 0 and the right-hand side of (2) is supposed to be convergent for some x = x0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 503 - 516
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Boas, R. P., Entire functions (New York, 1954).Google Scholar
2. Chaundy, T., The differential calculus (Oxford, 1935).Google Scholar
3. Doetsch, G., Handbuch der Laplace Transformationen, Vol. 1 (Basel, 1950).Google Scholar
4. Hobson, E. W., The theory of functions of a real variable, Vol. 2 (New York, 1957).Google Scholar
5. Jordan, C., Calculus of finite differences (New York, 1950).Google Scholar
6. Saltz, D., An inversion theorem for Laplace-Stieltjes transforms, Pacific J. Math., 10 (1960), 309–312.Google Scholar
7. Widder, D. V., The Laplace transform (Princeton, 1946).Google Scholar
8. Widder, D. V., A symbolic form of an inversion formula for the Laplace transform, Amer. Math. Monthly, 55 (1948), 489–491.Google Scholar
9. Whittaker, E. T. and Watson, G. N., A course in modern analysis (Cambridge, 1946).Google Scholar