Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chakravarti, I.M
1971.
Some properties and applications of Hermitian varieties in a finite projective space PG(N, q2) in the construction of strongly regular graphs (two-class association schemes) and block designs.
Journal of Combinatorial Theory, Series B,
Vol. 11,
Issue. 3,
p.
268.
Bose, R. C.
and
Shrikhande, S. S.
1972.
Geometric and pseudo-geometric graphs (q2+1,q+1,1).
Journal of Geometry,
Vol. 2,
Issue. 1,
p.
75.
Coxeter, H. S. M.
1974.
The equianharmonic surface and the Hessian polyhedron.
Annali di Matematica Pura ed Applicata,
Vol. 98,
Issue. 1,
p.
77.
Hubaut, Xavier L.
1975.
Strongly regular graphs.
Discrete Mathematics,
Vol. 13,
Issue. 4,
p.
357.
Kestenband, Barbu C.
1983.
Partitions of finite affine geometries into caps.
Linear and Multilinear Algebra,
Vol. 14,
Issue. 3,
p.
257.
Vecchi, Italo
1984.
Some results on coverings of galois spaces with ovoids and related bib designs.
Journal of Statistical Planning and Inference,
Vol. 10,
Issue. 2,
p.
219.
Chakravarti, I. M.
1988.
Coding Theory and Applications.
Vol. 311,
Issue. ,
p.
116.
Kestenband, Barbu C.
1988.
Partitioning projective planes into arcs.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 104,
Issue. 3,
p.
435.
Chakravarti, I. M.
1990.
Coding Theory and Design Theory.
Vol. 20,
Issue. ,
p.
35.
Yang, Benfu
and
Wei, Wandi
1990.
Finite orthogonal geometries with characteristic ≠ 2 and PBIB designs. I.
Linear Algebra and its Applications,
Vol. 134,
Issue. ,
p.
1.
Kestenband, Barbu C.
1992.
New families of balanced incomplete block designs with block size q + 1.
Journal of Statistical Planning and Inference,
Vol. 30,
Issue. 1,
p.
83.
Chakravarti, I.M.
1993.
Geometric construction of some families of two-class and three-class association schemes and codes from nondegenerate and degenerate Hermitian varieties.
Discrete Mathematics,
Vol. 111,
Issue. 1-3,
p.
95.
Cherdieu, J.P.
1995.
Exponential sums, codes, and Hermitian forms.
IEEE Transactions on Information Theory,
Vol. 41,
Issue. 6,
p.
1636.
Wan, Zhe-xian
1996.
Group Theory in China.
p.
182.
Wan, Zhe-xian
1997.
Geometry of classical groups over finite fields and its applications.
Discrete Mathematics,
Vol. 174,
Issue. 1-3,
p.
365.
Rodier, F
2000.
Nombre de points des surfaces de Deligne et Lusztig.
Journal of Algebra,
Vol. 227,
Issue. 2,
p.
706.
Wang, Kaishun
and
Wei, Hongzeng
2000.
GEOMETRIC CONSTRUCTION OF ASSOCIATION SCHEMES FROM DEGENERATE QUADRICS IN PROJECTIVE SPACES PG (2 v + δ + l − 1, F q ) FOR q ODD.
Acta Mathematica Scientia,
Vol. 20,
Issue. 1,
p.
35.
Cossidente, Antonio
and
Siciliano, Alessandro
2001.
On the Geometry of Hermitian Matrices of Order Three Over Finite Fields.
European Journal of Combinatorics,
Vol. 22,
Issue. 8,
p.
1047.
Cherdieu, J.-P.
Mercier, D.-J.
and
Narayaninsamy, T.
2001.
On the Generalized Weights of a Class of Trace Codes.
Finite Fields and Their Applications,
Vol. 7,
Issue. 2,
p.
355.
Mercier, Dany-Jack
2003.
Two codes related to hermitian forms.
Journal of Pure and Applied Algebra,
Vol. 179,
Issue. 3,
p.
273.
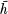 = hq is defined to be conjugate to h.
= hq is defined to be conjugate to h.

