Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ree, Rimhak
1956.
The existence of outer automorphisms of some groups.
Proceedings of the American Mathematical Society,
Vol. 7,
Issue. 6,
p.
962.
Ree, Rimhak
1958.
The existence of outer automorphisms of some groups. II.
Proceedings of the American Mathematical Society,
Vol. 9,
Issue. 1,
p.
105.
Losey, Gerald
1960.
On dimension subgroups.
Transactions of the American Mathematical Society,
Vol. 97,
Issue. 3,
p.
474.
Roseblade, J. E.
1962.
On Certain Classes of Locally Soluble Groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 58,
Issue. 2,
p.
185.
Losey, Gerald
1964.
A Class of Homomorphism Theories for Groupoids.
Proceedings of the Edinburgh Mathematical Society,
Vol. 14,
Issue. 2,
p.
129.
Sinha, Indranand
1966.
On the augmentation-maps of the subgroups of a group.
Mathematische Zeitschrift,
Vol. 94,
Issue. 3,
p.
193.
Swan, Richard G.
1967.
Representations of polycyclic groups.
Proceedings of the American Mathematical Society,
Vol. 18,
Issue. 3,
p.
573.
Zassenhaus, Hans
1969.
On linear noetherian groups.
Journal of Number Theory,
Vol. 1,
Issue. 1,
p.
70.
Riles, J.B.
1969.
The near Frattini subgroups of infinite groups.
Journal of Algebra,
Vol. 12,
Issue. 2,
p.
155.
Gruenberg, Karl W.
1970.
Cohomological Topics in Group Theory.
Vol. 143,
Issue. ,
p.
51.
Losey, Gerald
1970.
Are One-Sided Inverses Two-Sided Inverses in a Matrix Ring Over a Group Ring?.
Canadian Mathematical Bulletin,
Vol. 13,
Issue. 4,
p.
475.
Formanek, Edward
1970.
A short proof of a theorem of Jennings.
Proceedings of the American Mathematical Society,
Vol. 26,
Issue. 3,
p.
405.
Pickel, P. F.
1971.
Finitely generated nilpotent groups with isomorphic finite quotients.
Bulletin of the American Mathematical Society,
Vol. 77,
Issue. 2,
p.
216.
Pickel, P. F.
1971.
Finitely generated nilpotent groups with isomorphic finite quotients.
Transactions of the American Mathematical Society,
Vol. 160,
Issue. 0,
p.
327.
Kublanova, E. M.
1971.
Dimensional subgroups and their generalization.
Siberian Mathematical Journal,
Vol. 12,
Issue. 3,
p.
391.
Rips, E.
1972.
On the fourth integer dimension subgroup.
Israel Journal of Mathematics,
Vol. 12,
Issue. 4,
p.
342.
Sandling, Robert
1972.
Dimension subgroups over arbitrary coefficient rings.
Journal of Algebra,
Vol. 21,
Issue. 2,
p.
250.
Simonyan, L. A.
1972.
Some examples of Lie groups and Lie algebras.
Siberian Mathematical Journal,
Vol. 12,
Issue. 4,
p.
602.
Akasaki, Takeo
1972.
Idempotent ideals in integral group rings.
Journal of Algebra,
Vol. 23,
Issue. 2,
p.
343.
Parmenter, M. M.
and
Sehgal, S. K.
1973.
Idempotent elements and ideals in group rings and the intersection theorem.
Archiv der Mathematik,
Vol. 24,
Issue. 1,
p.
586.


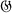 over a field of characteristic zero. We show that if Δ is the ideal of Γ spanned by all elements of the form G − 1, where G ∈
over a field of characteristic zero. We show that if Δ is the ideal of Γ spanned by all elements of the form G − 1, where G ∈