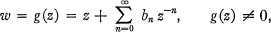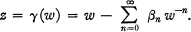Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Poole, J. T.
1966.
Coefficient extremal problems for schlicht functions.
Transactions of the American Mathematical Society,
Vol. 121,
Issue. 2,
p.
455.
Schober, Glenn
1977.
Coefficients of inverses of meromorphic univalent functions.
Proceedings of the American Mathematical Society,
Vol. 67,
Issue. 1,
p.
111.
Baernstein, Albert
and
Schober, Glenn
1980.
Estimates for inverse coefficients of univalent functions from integral means.
Israel Journal of Mathematics,
Vol. 36,
Issue. 1,
p.
75.
Siejka, Henryka
1986.
On meromorphic univalent functions omitting a disc.
Israel Journal of Mathematics,
Vol. 54,
Issue. 3,
p.
291.
Yang, Shanshuang
1994.
Estimates for coefficients of univalent functions from integral means and Grunsky inequalities.
Israel Journal of Mathematics,
Vol. 87,
Issue. 1-3,
p.
129.
Дубинин, Владимир Николаевич
and
Dubinin, Vladimir Nikolaevich
2005.
Лемма Шварца и оценки коэффициентов для регулярных функций со свободной областью определения.
Математический сборник,
Vol. 196,
Issue. 11,
p.
53.
Dubinin, V. N.
2014.
Asymptotic behavior of the capacity of a condenser as some of its plates contract to points.
Mathematical Notes,
Vol. 96,
Issue. 1-2,
p.
187.
Dubinin, V. N.
2014.
On the reduced modulus of the complex sphere.
Siberian Mathematical Journal,
Vol. 55,
Issue. 5,
p.
882.
Дубинин, Владимир Николаевич
and
Dubinin, Vladimir Nikolaevich
2014.
Асимптотическое поведение емкости конденсатора при стягивании некоторых его пластин в точки.
Математические заметки,
Vol. 96,
Issue. 2,
p.
194.