Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T12:28:22.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Enveloping Algebras of Semi-SimpleLie Algebras

Published online by Cambridge University Press:  20 November 2018

N. Jacobson
N. Jacobson*
Affiliation:
Yale University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper we studied systems of equations of the form

(1)

(2)

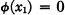
where as usual [a,b] = ab — ba and ϕ(λ) is a polynomial. Equations of this type have arisen in quantum mechanics. In our paper we gave a method of determining the matrix solutions of such equations. The starting point of our discussion was the observation that if the elements xi satisfy (1) then the elements xi, [xj,xk] satisfy the multiplication table of a certain basis of the Lie algebra 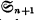of skew symmetric (n + 1) ⨯ (n + 1) matrices. We proved that if (2) is imposed as an added condition, then the algebra generated by the 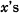has a finite basis, and we obtained the structure of the most general associative algebra that is generated in this way.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 2 , 1950 , pp. 257 - 266
Copyright
Copyright © Canadian Mathematical Society 1950

References

[1] Birkhoff, G., Representability of Lie algebras and Lie groups by matrices, Ann. of Math.,vol. 38 (1937), 526–532.Google Scholar
[2] Harish-Chandra, , On representations of Lie algebras, Ann. of Math., vol. 50 (1949), 900–915.Google Scholar
[3] Jacobson, N., Rational methods in the theory of Lie algebras, Ann. of Math., vol. 36 (1935),875–881.Google Scholar
[4] Jacobson, N., A note on non-associative algebras, Duke Math. Jour., vol. 3 (1937), 544–548.Google Scholar
[5] Jacobson, N., Lie and Jordan triple systems, Amer. Jour, of Math., vol. LXXI (1949), 149–170.Google Scholar
[6] Jacobson, N., The theory of rings, Mathematical Surveys II, New York, 1943.Google Scholar
[7] Morosov, W. W., On a nilpotent element in a semi-simple Lie algebra, Comptes Rendus de l'acad. des sciences de l'URSS (Doklady) vol. XXXVI, pp. 256–269.Google Scholar
[8] Weyl, H., Darstellung kontinuierlicher halb-einfacher Gruppen II, Math. Zeitsch., vol.27 (1925), 328–376.Google Scholar
[9] Witt, E., Treue Darstellung Liesche Ringe, J. Reine Angew. Math., vol. 177 (1937), 152–160.Google Scholar