Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mori, Tuyosi
1956.
On the group structure of Boolean lattices.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 32,
Issue. 7,
Walsh, Bertram
1967.
On characterizing Köthe sequence spaces as vector lattices.
Mathematische Annalen,
Vol. 175,
Issue. 4,
p.
253.
Bukhvalov, A. V.
1978.
Integral representation of linear operators.
Journal of Soviet Mathematics,
Vol. 9,
Issue. 2,
p.
129.
Arenson, E. L.
and
Kitover, A. K.
1992.
Compact disjointness preserving operators.
Functional Analysis and Its Applications,
Vol. 26,
Issue. 2,
p.
119.


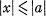 there exists a real number a for which x = aa. For every pair of discrete elements a, b ∈ R we have
there exists a real number a for which x = aa. For every pair of discrete elements a, b ∈ R we have 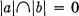 or there exists a real number a for which b = aa or a = ab.
or there exists a real number a for which b = aa or a = ab.