Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-20T14:40:28.029Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds for Solutions of a System of Linear Partial Differential Equations on Domains with Bergman-Silov Boundary

Published online by Cambridge University Press:  20 November 2018

Josephine Mitchell
Josephine Mitchell*
Affiliation:
MRC, University of Wisconsin and Pennsylvania State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The method of integral operators has been used by Bergman and others (4; 6; 7; 10; 12) to obtain many properties of solutions of linear partial differential equations. In the case of equations in two variables with entire coefficients various integral operators have been introduced which transform holomorphic functions of one complex variable into solutions of the equation. This approach has been extended to differential equations in more variables and systems of differential equations. Recently Bergman (6; 4) obtained an integral operator transforming certain combinations of holomorphic functions of two complex variables into functions of four real variables which are the real parts of solutions of the system

1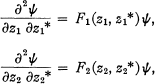

where z1, z1*, z2, z2* are independent complex variables and the functions Fj (J = 1, 2) are entire functions of the indicated variables.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 1272 - 1280
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Ahlfors, L. V., An extension of Schwarz's lemma, Trans. Amer. Math. Soc., 43 (1938), 359–364.Google Scholar
2. Bergman, S., Über eine in gewissen Bereichen gilltige Integraldarstellung der Funktionen zweier komplexer Variablen, Math. Z., 89 (1934), 76–94, 605-608.Google Scholar
3. Bergman, S., Bounds for analytic functions in domains with a distinguished boundary surface, Math. Z., 63 (1955), 173–194.Google Scholar
4. Bergman, S., Bounds for solutions of a system of partial differential equations, J. Rational Mech. and Anal., 5, (1956), 993–1002.Google Scholar
5. Bergman, S., Sur les fonctions orthogonales de plusieurs variables complexes (Paris, 1947).Google Scholar
6. Bergman, S., Integral operators in the theory of linear partial differential equations (Berlin, 1961).Google Scholar
7. Bergman, S. and Schiffer, M., Properties of solutions of a system of partial differential equations, Studies in Math, and Mech. presented to Richard von Mises (New York, 1954), 79–87.Google Scholar
8. Carathéodory, C., Conformai representation (Cambridge, 1941).Google Scholar
9. Charyński, Z., Bounds for analytic functions of two complex variables, Math. Z., 75 (1961), 29–35.Google Scholar
10. Gilbert, R. P., Some properties of generalized axially symmetric potentials, Amer. J. Math., 84 (1962), 475–484.Google Scholar
11. Kelley, J. L., General topology (Princeton, N.J., 1955).Google Scholar
12. Mitchell, J., Properties of harmonic functions of 3 real variables given by Bergman-Whittaker operators, Can. J. Math., 15 (1963), 157–168.Google Scholar
13. Śladkowska, J., Bounds of analytic functions of two complex variables in domains with the Bergman-Silov boundary, Pacific J. Math., 12 (1962), 1435–1451.Google Scholar