No CrossRef data available.
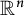 $\mathbb {R}^n$
$\mathbb {R}^n$Published online by Cambridge University Press: 13 September 2021
We determine the distance (up to a multiplicative constant) in the Zygmund class
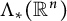 $\Lambda _{\ast }(\mathbb {R}^n)$
to the subspace
$\Lambda _{\ast }(\mathbb {R}^n)$
to the subspace
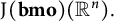 $\mathrm {J}_{}(\mathbf {bmo})(\mathbb {R}^n).$
The latter space is the image under the Bessel potential
$\mathrm {J}_{}(\mathbf {bmo})(\mathbb {R}^n).$
The latter space is the image under the Bessel potential
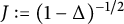 $J := (1-\Delta )^{{-1}/2}$
of the space
$J := (1-\Delta )^{{-1}/2}$
of the space
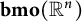 $\mathbf {bmo}(\mathbb {R}^n)$
, which is a nonhomogeneous version of the classical
$\mathbf {bmo}(\mathbb {R}^n)$
, which is a nonhomogeneous version of the classical
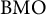 $\mathrm {BMO}$
. Locally,
$\mathrm {BMO}$
. Locally,
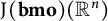 $\mathrm {J}_{}(\mathbf {bmo})(\mathbb {R}^n)$
consists of functions that together with their first derivatives are in
$\mathrm {J}_{}(\mathbf {bmo})(\mathbb {R}^n)$
consists of functions that together with their first derivatives are in
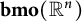 $\mathbf {bmo}(\mathbb {R}^n)$
. More generally, we consider the same question when the Zygmund class is replaced by the Hölder space
$\mathbf {bmo}(\mathbb {R}^n)$
. More generally, we consider the same question when the Zygmund class is replaced by the Hölder space
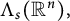 $\Lambda _{s}(\mathbb {R}^n),$
with
$\Lambda _{s}(\mathbb {R}^n),$
with
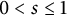 $0 < s \leq 1$
, and the corresponding subspace is
$0 < s \leq 1$
, and the corresponding subspace is
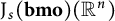 $\mathrm {J}_{s}(\mathbf {bmo})(\mathbb {R}^n)$
, the image under
$\mathrm {J}_{s}(\mathbf {bmo})(\mathbb {R}^n)$
, the image under
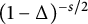 $(1-\Delta )^{{-s}/2}$
of
$(1-\Delta )^{{-s}/2}$
of
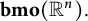 $\mathbf {bmo}(\mathbb {R}^n).$
One should note here that
$\mathbf {bmo}(\mathbb {R}^n).$
One should note here that
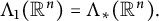 $\Lambda _{1}(\mathbb {R}^n) = \Lambda _{\ast }(\mathbb {R}^n).$
Such results were known earlier only for
$\Lambda _{1}(\mathbb {R}^n) = \Lambda _{\ast }(\mathbb {R}^n).$
Such results were known earlier only for
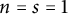 $n = s = 1$
with a proof that does not extend to the general case.
$n = s = 1$
with a proof that does not extend to the general case.
Our results are expressed in terms of second differences. As a by-product of our wavelet-based proof, we also obtain the distance from
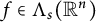 $f \in \Lambda _{s}(\mathbb {R}^n)$
to
$f \in \Lambda _{s}(\mathbb {R}^n)$
to
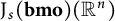 $\mathrm {J}_{s}(\mathbf {bmo})(\mathbb {R}^n)$
in terms of the wavelet coefficients of
$\mathrm {J}_{s}(\mathbf {bmo})(\mathbb {R}^n)$
in terms of the wavelet coefficients of
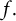 $f.$
We additionally establish a third way to express this distance in terms of the size of the hyperbolic gradient of the harmonic extension of f on the upper half-space
$f.$
We additionally establish a third way to express this distance in terms of the size of the hyperbolic gradient of the harmonic extension of f on the upper half-space
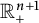 $\mathbb {R}^{n +1}_+$
.
$\mathbb {R}^{n +1}_+$
.
First author is supported by the Finnish Academy grant 1309940. Second author is supported by the Generalitat de Catalunya grant 2017 SGR 395, the Spanish Ministerio de Ciencia e Innovación projects MTM2014-51824-P and MTM2017-85666-P, and the European Research Council project CHRiSHarMa no. DLV-682402.