No CrossRef data available.
Article contents
Cubic Twin Prime Polynomials are Counted by a Modular Form
Published online by Cambridge University Press: 09 January 2019
Abstract
We present the geometry behind counting twin prime polynomials in 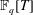 $\mathbb{F}_{q}[T]$ in general. We compute cohomology and explicitly count points by means of a twisted Lefschetz trace formula applied to these parametrizing varieties for cubic twin prime polynomials. The elliptic curve
$\mathbb{F}_{q}[T]$ in general. We compute cohomology and explicitly count points by means of a twisted Lefschetz trace formula applied to these parametrizing varieties for cubic twin prime polynomials. The elliptic curve 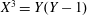 $X^{3}=Y(Y-1)$ occurs in the geometry, and thus counting cubic twin prime polynomials involves the associated modular form. In theory, this approach can be extended to higher degree twin primes, but the computations become harder.
$X^{3}=Y(Y-1)$ occurs in the geometry, and thus counting cubic twin prime polynomials involves the associated modular form. In theory, this approach can be extended to higher degree twin primes, but the computations become harder.
The formula we get in degree 3 is compatible with the Hardy–Littlewood heuristic on average, agrees with the prediction for 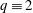 $q\equiv 2$ (mod 3), but shows anomalies for
$q\equiv 2$ (mod 3), but shows anomalies for 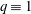 $q\equiv 1$ (mod 3).
$q\equiv 1$ (mod 3).
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
The authors acknowledge support provided by DAAD-Programm 57271540 Strategische Partnerschaften (supported by BMBF). The first author was partially supported by a grant from the Israel Science Foundation.


