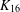Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T00:09:18.066Z Has data issue: false hasContentIssue false
  • English
  • Français

PERFECT 1-FACTORISATIONS OF $K_{16}$

Part of: Graph theory Designs and configurations

Published online by Cambridge University Press:  07 August 2019

MICHAEL J. GILL Open the ORCID record for MICHAEL J. GILL [Opens in a new window]  and
IAN M. WANLESS Open the ORCID record for IAN M. WANLESS [Opens in a new window]
MICHAEL J. GILL
Affiliation:
School of Mathematics, Monash University, Vic 3800, Australia email [email protected]
IAN M. WANLESS*
Affiliation:
School of Mathematics, Monash University, Vic 3800, Australia email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report the results of a computer enumeration that found that there are 3155 perfect 1-factorisations (P1Fs) of the complete graph 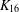$K_{16}$. Of these, 89 have a nontrivial automorphism group (correcting an earlier claim of 88 by Meszka and Rosa [‘Perfect 1-factorisations of 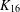$K_{16}$ with nontrivial automorphism group’, J. Combin. Math. Combin. Comput. 47 (2003), 97–111]). We also (i) describe a new invariant which distinguishes between the P1Fs of 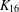$K_{16}$, (ii) observe that the new P1Fs produce no atomic Latin squares of order 15 and (iii) record P1Fs for a number of large orders that exceed prime powers by one.

Keywords

perfect 1-factorisationHamilton cycleatomic Latin squaretrainquotient coset starter

MSC classification

Primary: 05C70: Factorization, matching, partitioning, covering and packing
Secondary: 05B15: Orthogonal arrays, Latin squares, Room squares
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 2 , April 2020 , pp. 177 - 185
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by an Australian Government Research Training Program (RTP) Scholarship and by ARC grant DP150100506.

References

Bryant, D., Maenhaut, B. and Wanless, I. M., ‘New families of atomic Latin squares and perfect one-factorisations’, J. Combin. Theory Ser. A 113 (2006), 608–624.Google Scholar
Colbourn, C. J. and Colbourn, M. J., ‘Combinatorial isomorphism problems involving 1-factorizations’, Ars Combin. 9 (1980), 191–200.Google Scholar
Dinitz, J. H. and Garnick, D. K., ‘There are 23 non-isomorphic perfect one-factorisations of K 14’, J. Combin. Des. 4 (1996), 1–4.Google Scholar
Kaski, P., Medeiros, A. D. S., Östergård, P. R. J. and Wanless, I. M., ‘Switching in one-factorisations of complete graphs’, Electron. J. Combin. 21(2) (2014), #P2.49.Google Scholar
Meszka, M., ‘There are 3155 nonisomorphic perfect 1-factorizations of $K_{16}$’, submitted for publication.Google Scholar
Meszka, M. and Rosa, A., ‘Perfect 1-factorizations of K 16 with nontrivial automorphism group’, J. Combin. Math. Combin. Comput. 47 (2003), 97–111.Google Scholar
Pike, D. A., ‘A perfect 1-factorisation of K 56’, J. Combin. Des. 27 (2019), 386–390.Google Scholar
Rosa, A., ‘Perfect 1-factorizations’, Math. Slovaca 69 (2019), 479–496.Google Scholar
Seah, E., ‘Perfect one-factorizations of the complete graph—a survey’, Bull. Inst. Combin. Appl. 1 (1991), 59–70.Google Scholar
Wallis, W. D., One-factorizations (Kluwer Academic, Dordrecht, Netherlands, 1997).Google Scholar
Wanless, I. M., ‘Atomic Latin squares based on cyclotomic orthomorphisms’, Electron. J. Combin. 12 (2005), #R22.Google Scholar
Wanless, I. M., Author’s homepage, http://users.monash.edu.au/∼iwanless/data/P1F/newP1F.html.Google Scholar
Wanless, I. M. and Ihrig, E. C., ‘Symmetries that Latin squares inherit from 1-factorizations’, J. Combin. Des. 13 (2005), 157–172.Google Scholar
Wolfe, A. J., ‘A perfect one-factorization of K 52’, J. Combin. Des. 17 (2009), 190–196.Google Scholar