Introduction
Flow records of meltwater runoff provide some information about the movement of water through the ice and about glacial ablation. In summer, the discharge has a notable diurnal variation superimposed on a base flow whose volume changes more slowly. In addition, the peak discharge comes a few hours after the peak in glacial ablation. As summer advances, however, the daily rise and fall in discharge becomes more rapid and the lag time decreases. Total daily discharge usually reaches its maximum in late July or early August. When summer snowfall inhibits melting, the diurnal variation in discharge ceases and the base flow attains its former level within a few days.
As for an analysis of discharge curves, Reference EllistonElliston (1973) inferred that at least half of the meltwater was retained for at least 1 day within Gornergletscher, Switzerland. Reference LangLang (1973) found the lag time needed to give maximum correlation between daily discharge and air temperature. He concluded that water spent, on average, 2–3 days in Aletschgletscher, the largest glacier in Switzerland, in early summer but only 1 day in August. Of course, the lag time is not uniform for different glaciers. In addition, the sensitivity of the meltwater response to air temperature changed over the ablation season, resulting in differential contributions of meltwater runoff to the base flow. The size, shape and characteristics of the englacial channels often affect the fluctuation of the meltwater runoff. Past research (Reference PatersonPaterson, 1994) suggests that the reduction of the time interval between the daily peaks of discharge and meltwater runoff as the season progresses results partly from development of the englacial drainage system and partly from the reduction of the thickness and extent of snow cover.
Reference LettenmaierLettenmaier (1980) has applied time-series analysis in hydrologic investigations. His research has been oriented essentially toward hydrologic forecasting, completion of data and estimation of parameters for stochastic models, and analyzed primarily the univariate spectral and the cross-correlation functions. Since the 1990s, many people have used cross-correlation functions and cross-spectral function to analyze different questions by going deeply into the other functions of the cross-spectral analysis, such as the coherence function, gain function and phase functions. Reference Padilla and Pulido-BoschPadilla and Pulido-Bosch (1995) have successfully applied this method to the study of karstic aquifers to characterize the transformations in these systems between the input function (precipitation) and the output function (discharge). Reference Molénat, Davy, Gascuel-Odoux and DurandMolénat and others (1999) have used this method to characterize the major process that governs water and nitrate by means of the observed frequency transfer function on three agricultural catchments. However, to our knowledge, no researchers have used this method to study glacio-hydrology to analyze the temporal character of the fluctuations of the meltwater runoff and changes in air temperature. This paper focuses on the fluctuation of the discharge series and air-temperature series based on our field investigation. We analyze the relation using correlation and cross-spectral analysis to formulate some concrete relationships between these parameters.
Keqikaer Glacier
Tuomuer mountain is located in China’s western Tien Shan, in the Xingjiang Uigur Autonomous Region. It is the highest peak in the Tien Shan range. The glaciers in the Tuomuer mountain area cover a total area estimated at about 3850 km2, and the water equivalent of the glaciers is >4200 x 108m3, or three times the water equivalent of the glaciers in the Qomolangma (Mount Everest) area (Reference Su, Sun, Wang, Su and KangSu and others, 1985). Hence, the glaciers are capable of releasing a large amount of meltwater, which is the main source of water in the arid region of western China. In order to examine how glaciers respond to climatic changes and the hydrological characteristics of the glaciers in this area, the authors and others have conducted a survey in this region since June 2003 (Reference Xie, Ding and LiuXie and others, 2004). The emphasis of this survey is the Ataoyilake river basin. Three glaciers are located in this basin, and Keqikaer glacier (also named Keqicar Baqi glacier) is the largest of the three.
Keqikaer glacier is located on the south slope of Tuomuer mountain, approximately 60 km north of Akzo city, Xinjiang Uigur Autonomous Region, China (41˚48.77’N, 80˚10.20’ E). It is a large dendritic mountain valley glacier that extends from 6435 to 3020ma.s.l. with a length of 25.1 km and an area of 83.6 km2 (Fig. 1). Beneath the snowline, the tongues are generally about 1−3 km wide and >19 km long. Therefore, the ablation area of Keqikaer glacier is relatively large. Air temperature on the glacial tongues is relatively high during the ablation period. For example, the average temperature from 1 May to 30 September 2004 reached 1.8˚C at 4250 ma.s.l. and 4.5˚C at 3750 ma.s.l. Hence, Keqikaer glacier is favorably situated to provide sensible heat for glacial ablation that is consequently very rapid on the surface of the glacial tongues. For example, ablation reaches 1850−3650 mm w.e., and the daily ablation could reach 90 mm on the glacial tongue at an altitude of 3020−4350 m from 1 May to 30 September 2004. There are many surface channels on the glacial tongue, and because of the erosion by meltwater and uneven melting the melt holes, funnels and under ditches are formed within the glacier, and runoff systems are widely distributed throughout the glacier. However, most of the meltwater flows out of Keqikaer glacier by an ice cavern, which is located under the glacial terminus.

Fig. 1. Location of Keqikaer glacier, showing the position of the hydrometric and meteorological monitoring stations.
During our scientific survey, a temporary hydrometric station was established in the vicinity of the glacial terminus at 2967 m a.s.l., recording a discharge series at an interval of 15 min over the last 2 years. Air temperature, wind direction, relative humidity and precipitation are observed by two automatic weather stations (AWSs) that are set on the glacier; one is set on the upper surface moraine of the terminus with an altitude of 3750 m (AWS-A, at 3150 m a.s.l. in 2003), and the other is set on the border moraine near the snowline at 4250 ma.s.l. (AWS-B). Meteorological factors are recorded every 1 hour over the period of this study.
Method
Conventional studies of time series by correlation and spectral methods of analysis use both univariate and cross-analysis (Reference HuangHuang, 1983). Univariate analysis characterizes the individual structure of the time series; the functions applied are autocorrelation (in the time domain) and spectral density (in the frequency domain). Cross-analysis characterizes the transformation of an input function into an output function. The cross-correlation function is analyzed in the time domain, and the cross-amplitude, phase, coherence and gain functions are analyzed in the frequency domain. In this study, we consider temperature as the input function, and meltwater runoff as the output function, with the intent of going deeply into the interpretation of the results obtained with correlation and cross-spectral analysis.
By following the spectral theory (Reference HuangHuang, 1983), there are two discretized chronological series, xt (x 1 , x2 x3 … xn), which is responsible for producing the second series, yt (y 1 , y2 y3 … yn), where n is the number of data pairs available. The spectral-density functions of the series xt can be expressed as

where rx(k) is the function of autocorrelation of the xt series, expressed as


and the cross-correlation functions obtained with the two series are
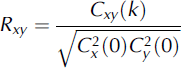

where




in which m is a truncation point, for k = 0, 1, 2 … m and ![]() and
and ![]() are the means of the series xt and yt ,respectively. The spectral-density function can be obtained from the cross-correlation function by Fourier transform, expressed as (Reference HuangHuang, 1983; Reference Ding and DengDing and Den, 1988):
are the means of the series xt and yt ,respectively. The spectral-density function can be obtained from the cross-correlation function by Fourier transform, expressed as (Reference HuangHuang, 1983; Reference Ding and DengDing and Den, 1988):
in which i and * represent ![]() and the plural-conjugate separately, and Pxy(f) is the co-spectrum and Qxy(f) is the quadrature spectrum. These are expressed as:
and the plural-conjugate separately, and Pxy(f) is the co-spectrum and Qxy(f) is the quadrature spectrum. These are expressed as:


in which Dk is a weighting function necessary to overcome bias in the coefficients of Pxy(f) and Qxy(f). Of the many weighting functions, Hanning weighting functions and Hamming-Tukey weighting functions are usually used in the analysis of hydrological series (Reference HuangHuang, 1983). Hanning weighting functions are expressed as:

By using Pxy(f) and Qxy(f), the cross-amplitude and phase functions for the frequency can be calculated and the expressions become:

With the cross-amplitude function (CAF) and the simple-density spectrum, new functions can be defined, such as the coherence function, 7 xy (f), and the gain function, Gxy(f), expressed as:


where Sx(f) and Sy(f) are the spectral-density functions of the series x and y, respectively.
In this paper, we took air-temperature data series as the input function, separately, and discharge series as the output function. From the standpoint of its application to a hydrological series, the cross-amplitude function, Ψ(f), can be associated with the duration of the impulse response function and indicates the filtering of the periodic components of air temperature and precipitation. The phase function, 0(0, shows the delay, for different frequencies, between the air temperature and the meltwater runoff. Its variation range is 2π, generally between –π and π. An excessive attenuation of the input data for the system appears in the cross-amplitude and gain functions; the mean delay, d, can be obtained by the slope (equal to 2π) of the line of best fit to:
The coherence function shows whether variations in the output series respond to the same type of variations in the input series or not, and indicates the correlation in the periodic variables. Values of coherence function are limited to the range between 0 and 1. With the majority of values near 1, a more powerful correlation between the input and output factors is realized. The gain function expresses the amplification or attenuation of the input data, which depends on the intervening system. If the gain function is >1, it shows that the fluctuation of the input factor amplifies that of the output factor at the right frequency; whereas, if the gain function is < 1 , the fluctuation of the input factor attenuates that of the output factor.
Results
By means of correlation and cross-spectral analysis, this research allowed a study of the relationship between air temperature and meltwater runoff in different months of the ablation period. Data have been selected from the 1st to the 30th for every month, and the calculated hourly discharge of the meltwater runoff for each day was utilized. Thus there are 720 sets of temperature and discharge data in every month. Temperature data series are derived from the AWS at 3750 m a.s.l. Figure 2 is the hydrograph of the daily discharge series observed at the glacial hydrometric station and the air-temperature series on Keqikaer glacier from 1 May to 30 September 2004. It is clear that daily discharge has a lag time relative to the temperature during the entire ablation period. From this figure, we can see that when temperature is low, the discharge is less and when the air temperature is high for several days, the discharge increases, often approaching a flood peak for this area. However, duration of 1 day is the basic period of fluctuation of the discharge and air temperature.

Fig. 2. Hydrograph of the daily discharge and air temperature of the ablation period in 2004.
The discharge and air-temperature data series had to be filtered in order to eliminate the linear component because only a stationary time series could be analyzed by spectral analysis (Reference HuangHuang, 1983). In addition, we needed to standardize the data series to compare the results of different months. Standardization was accomplished by dividing the original data by the root-mean-square (rms) error S, expressed as:

For the standardized data series (X1,X2, •••Xn), the rms error and square deviation are equal to 1. The cross-spectral analysis of the standardized data series in conjunction with the original data series gives a result that is equivalent to 1 / S 2.
The results for the different months of our study period obtained by using the correlation and cross-spectral analyses are presented in Figure 3. We will interpret the amplitude function, gain function, coherency function and phase function in this part of the paper. The cross-amplitude function distinctly shows the curve forms of the prominent peaks at frequencies of 0.22 and 0.041 (Fig. 3a), which indicated that the discharge and air temperature have a common periodicity of 1 and 2 days respectively. As we can see from Figure 2, 1 day is the basic fluctuation period of the discharge and air temperature. The gain function shows the same results: discharge’s fluctuation is amplified by the fluctuation of air temperature at the frequencies 0.22 and 0.041, but discharge’s fluctuation is attenuated at other frequencies (Fig. 3c). For the period of measurement and analysis reported here using the cross-amplitude function and gain function, the discharge of July and August is apparently more influenced by air temperature than that of June and September. This conclusion can also be drawn from the coherence function. Figure 3b shows that there is not as great a correlation for the frequencies in June and September compared to those in July, August and May. The correlation, observable in the coherence function at those frequencies, with which discharge and air temperature fluctuates periodically, is greater than in other frequencies, especially in May. So we come to the conclusion that discharge of meltwater runoff has greater sensitivity to air temperature in May, July and August than in June and September. The mean lag time calculated according to Equation (14) by the result of the phase function in different months shows the lag time exceeds 1day in May and September but falls short of 1 day in other months, and it decreases from May to August, but increases in September (Fig. 4).

Fig. 3. Plots of the functions obtained by means of cross-spectral analysis: (σ) amplitude function; (b) coherence function; and (c) gain function.

Fig. 4. The lay time obtained by phase function in different months.
Discussions and Conclusion
For the period of our study, the research suggests that the ablation of Kaqikaer glacier begins during the middle 10 days of April and stops at the end of October, with the discharge of meltwater runoff changing along with the variations of the ablation area during different months. Our research further indicated that the ablation area of the glaciers at the south slope of Tuomuer mountain is smaller in May and September than in July and August (Reference Su, Sun, Wang, Su and KangSu and others, 1985). It takes only 1–2 hours for the meltwater to reach the hydrometric station from 3750 m a.s.l, and 3–4 hours from 4250 m a.s.l. The proportion of the rapid flow which formed in the ablation area is small in May, June and September, while it is large in July and August because of not only low air temperature but also the small ablation area. Thus the fluctuation of the rapid flow is greater in July and August than in May, June and September. For May, the thaw of snow is sensitive to the variation of air temperature, and the snow meltwater is a leading resource of runoff volume, so the meltwater runoff has greater sensitivity to the air temperature as disclosed by the coherence function and gain function.
In May and September, the bare ablation area is small; the water provided by the snow-cover area is large, and needs more time to drain from the glacier. However, in July and August, the proportion of meltwater provided by the snow-cover area is small and the lag time is short. June is a special month that calls for further discussion. Meltwater runoff is small and air temperature is low in June, but the ice meltwater in the ablation area has produced most water, because snow meltwater of the ablation area has drained away in May. The proportion of rapid flow is small, so the meltwater runoff has little sensitivity to the fluctuation of air temperature. The meltwater provided by the snow-cover area is small, so the lag time is short in this month.
In this paper, cross-spectral analysis has been used to analyze the fluctuation of the glacial meltwater runoff and its response to the air temperature, and the method is successfully applied to evaluate the sensitivity of the discharge to air temperature and to calculate the lag time in different months. Compared with a physical-math model, the theory is simple, the conception is clear and the parameters are few. From Keqikaer glacier, we arrived at the conclusion that the meltwater runoff has greater sensitivity to air temperature in May, July and August than in June and September. The lag time is shorter in June, July and August than in May and September.
Acknowledgements
Thanks to E. Mosley-Thompson and D. Cecil for helpful comments and careful revisions that greatly improved the paper. This work was supported by the Chinese National Fundamental Research Program (No. 40371026) and the Knowledge Innovation Project of the Chinese Academy of Sciences (No. KZCX3-SW-345 and KZCX3-SW-351).






