1. Motivation
Snow avalanches can destroy large tracts of mountain forests. This fact was clearly evident during the extreme avalanche winters of 1951 and 1999, when large avalanches easily demolished tree stands of various ages (SLF, 1951, 2000). Quite often the fractured tree debris was entrained into the snow flow. Avalanche deposits were strewn with large tree trunks, lopped branches, wood fragments, root clusters and eroded soil (Fig. 1).
Fig. 1. Avalanche deposits at Evolene, Switzerland. Mote the size of the fractured tree trunks and amount of wood debris. The runout distance of this avalanche was correctly predicted without considering the influence of the forest.
The importance of protective forests in preventing avalanches from starting has been studied by Reference De QuervainDe Quervain (1979), Reference SalmSalm (1979) and Reference Gubler and RychetnikGubler and Rychetnik (1991). The purpose of these works was to establish the tree spacing required to stabilize the snowpack on forested slopes. The inclusion of forests in avalanche-dynamics calculations, however, has not been studied in detail. This is understandable, given that there are even now still many unanswered questions dealing with snow flow in open, i.e. unforested, terrain.
The Swiss Guidelines on avalanche-runout calculation specify that the velocity-dependent friction parameter used in model calculations can be increased on forested slopes (Reference Salm, Burkard and GublerSalm and others, 1990). The dry Coulomb friction values remain unchanged. This procedure decreases the predicted terminal velocity of the avalanche significantly, yet decreases the predicted runout distances only slightly (Reference Bartelt, Salm and GruberBartelt and others, 1999). This empirical approach is based on extensive model calibration (Reference Buser and FrutigerBuser and Frutiger, 1980). Since these model calculations have been calibrated using observed runout distances, the requisite of decreasing the velocity- dependent friction can clearly be questioned. Furthermore, in practice hazard maps are prepared by using model calculations that assume the forest no longer exists to slow the avalanche down. The safe assumption must always be made that a tree stand has been destroyed by a previous avalanche.
In summary, the problem of avalanche flow in forests is both highly complex and has little practical priority. Nonetheless, the question of why snow avalanches destroy forests so easily is of great natural interest. To be able to quantitatively understand the problem of avalanche flow in forests provides valuable insight into the very nature of the destructive force of snow avalanches. In addition, calculation guidelines must be based on rational procedures that include the effect of tree stands. Procedures must be developed that account for avalanche flow in forests in order to back-calculate observed avalanche events, a particularly important task after the European avalanche winter of 1999. In future, it might also be possible to develop strategies to maintain protective forests in avalanche tracks that optimize their protective capacity and which are both economically efficient and ecologically sound.
The purpose of this paper is therefore to calculate the deceleration of flowing and powder-snow avalanches caused by fracturing, overturning and entraining trees as functions of forest parameters such as mean tree spacing and tree parameters such as height, girth, branchiness and root-system strength. We will apply the principle of conservation of energy to a center-of-mass avalanche model to derive friction formulas for the mean deceleration of snow avalanches. This is a first step in developing friction laws for advanced numerical models. The principal problem that must be solved is to relate the mechanical properties of trees to the dynamics of snow avalanche flow.
An important distinction must be made from the beginning between avalanche flow force and flow energy. We assume that the avalanches are sufficiently large and fast-moving to enable the forces they apply to the trees to fracture or overturn them. We do not consider how the avalanche force is applied to the trees. In fact, the trees which are entrained in the flow will smash into other trees, applying the force of the avalanche in an arbitrary and completely incalculable manner. Many foresters believe that this “battering-ram” effect is the main cause of forest destruction. In the following, we will assume that this destructive force will always be enough to destroy the remaining trees. How the force is applied is immaterial to our analysis. We are not interested in the fracture stress or overturning moment which must be overcome, rather in the fracture energy. Small or slow-moving avalanches which, because they exert small forces, do not destroy the forest are of little interest. If the entrained trees block the path of the avalanche by becoming tangled in the standing trees, the avalanche at that moment simply does not have the force to destroy the forest. Of course the locked tree trunks will increase the internal flow resistance. But this will only occur when the avalanche is already close to stopping.
The above explanation is central to understanding why mountain forests offer little protection against snow avalanches once the avalanches have already started and reached a critical flow energy. It reveals the gist of our calculations and explains the massive forest destruction during the winters of 1951 and 1999: trees can resist large forces, but on breaking consume little of the avalanche’s flow energy. In the following we will try to prove this supposition. At what critical flow velocity the trees break or overturn must be the topic of another work.
2. Mathematical Description of a Forest and Principal Modes of Forest Failure
We assume, based on our field observations, that a forest is damaged or destroyed according to one of the following four causes:
Tree fracture and entrainment
A flowing avalanche fractures and entrains the trees in the flow. The fracture energy, uf is assumed to be linearly proportional to the the trunk’s cross-sectional area. Values of uf can be found in Reference SellSell (1987). We will assume that the tree trunks have a constant girth of radius rt. The girth is constant over the entire tree height, ht. The mass of the tree is mt. For the moment, we will assume that the tree fractures at the base of the trunk and thus the entire tree is entrained. The center of mass of the tree is denoted by Zt. The number of trees entrained per unit time, nt, is given by (1) the mean tree spacing in the direction of flow d1, (2) the tree spacing along the width of the avalanche, dw, (3) the avalanche’s speed u and (4) the width, w, of the avalanche (see Fig. 2),
Fig. 2. Definition of forest and tree parameters. The mean tree spacing is given by d1 and dw. We assume trunks of constant circular cross-section with radius rt. The avalanche with width w is flowing with velocity u.
Tree overturning
An avalanche overturns trees. The breaking energy is approximated by assuming that the failure stress on the overturning slip surface is given by a Mohr-Coulomb failure criterion:
where τf is the shear stress acting on the wedge failure surface and σz is the overburden stress. The parameters c and 6 are the cohesion and internal flow friction of the mountain soil. The overturning wedge is a half-cylinder with radius rf and length 2rf. Overturning is thus defined by three parameters, the internal friction angle 6 of the soil, the soil cohesion, c, and the failure radius of the root cluster, rf. The overburden stress is clearly a function of tree mass.
Tree overturning with entrainment
Observations of avalanche deposits reveal that entire overturned trees are entrained in the flow and are carried long distances (Fig. 3). In this case, the influence of overturning and that of entrainment are added to find the total avalanche deceleration.
Fig. 3. The tree is overturned. The failure surface is described by Mohr-Coulomb yield surface, τ = c + σz tan δ.
Trunk fracture and branch lopping
Powder-snow avalanches will often fracture the trunks of trees but will not entrain them in the avalanche flow. In this case, we consider the deceleration caused by fracture alone. Often the trunks will remain standing but are completely stripped of their branches. Tree lopping by powder-snow avalanches is a special case which requires the introduction of an additional tree parameter, the mean branch spacing, db. The number of branches fractured per tree per unit time is
The branches have mean length, lb. We will assume that the fracture energy per cross-sectional area of the branches is the same as that of the trunk. This is probably not the case, but we have found no experimental data to allow a more realistic modeling.
In summary, the above failure modes involve three physical processes: fracture, overturning and entrainment. The avalanche decelerations produced by each of these processes are derived in the following sections.
3. Energy Analysis
We determine the motion of an avalanche moving down a slope of constant angle ψ between two discrete times, t0 and h. At time t0 the avalanche is moving with velocity u0 and has flow height h0 and length lo (see Fig. 4). At time t1 the avalanche has flow velocity u1 and height h1 and length l1 (see Fig. 5). Between time t0 and t1 (time interval At) the avalanche changes velocity by Au:
Fig. 4. An avalanche with height h0 and length l0 is flowing with velocity u0. It enters a tree stand with tree spacing d1, tree mass mt, tree height ht and tree center of mass, Zt. The center of mass of the total tree stand entrained within the time period Δt is Ze.
Fig. 5. After the time period At, the avalanche is now moving with velocity u1=u0 + Δu and is located at height Z1. The avalanche has entrained Ame tree mass.
The avalanche penetrates the distance u0Δt into the forest. Over the same time interval, the center of mass of the avalanche moves downwards from height Z0 to Z1. Application of the principle of conservation of energy at positions 0 and 1 leads to
where
is the energy required per unit time to either fracture or overturn the trees. Values for E will be derived in sections 4 and 5. In the following, the energy equation will be solved to find Δn/Δt, the avalanche deceleration. The center of mass of the avalanche at position 1 defined in relation to Z0
is
For the special case when
and when the avalanche does not change mass (m1 = m0) or shape (Δl = Δh = 0), the trivial solution is obtained,
This result is found by substituting Equations (4) and (6) into Equation (5) and neglecting all second-order terms, i.e. assuming terms such as (Δt)2 or (ΔuΔt) are zero.
4. Tree Entrainment
Because it entrains debris, the avalanche grows in mass and volume. The change in mass over the time interval At is
Subsequently, the mass of the avalanche at position 1 is
The mean flow density of the avalanche is denoted pa. The volume of the avalanche is
and thus the volume change within the time interval At is
Assuming small time-steps, the last (second-order) term in Equation (11) will be small and neglected in future calculations. The width of the avalanche does not change. We define a parameter 7 such that
Since the trees are incompressible, the change in volume of the avalanche over the time interval At is
where Vt is the tree volume. We express the tree volume as
where 0t is the volumetric tree content defined over the volume
Thus, the change in height and length of the avalanche can be calculated according to
and
The dimensionless parameter 7 allows for different rates of avalanche growth in the length and height directions. For 7 = 0, the entrained tree mass increases exclusively the length of the avalanche. For 7 = 1 the entrained tree mass increases the avalanche flow height.
The energy-balance Equation (5) can now be written
where the position of the center of mass Ze (entrained tree mass) is defined according to Figure 5 and given by
Note that the potential energy of the trees is considered in the term ΔmegZe. For the moment, we will assume that
is zero in order to study the deceleration of the avalanche caused by tree entrainment alone.
The deceleration of an avalanche caused by tree entrainment can be found by substituting the equations for Ul (Equation (4)), Z1 (Equation (6)), Δm6 (Equation (8)) and Ze (Equation (19)) into Equation (18):
where
The derivation of Equation (20) again neglects all second-order terms.
The equation for aet contains the term,
indicating that mass entrainment introduces a velocity-dependent deceleration. The term kgZt
represents the avalanche acceleration (note sign) caused by the falling trees, i.e. it represents potential energy of the trees that is added to the flow energy of the avalanche. The remaining terms in the equation arise because the center of mass of the avalanche moves as the avalanche grows in length and height.
5. Tree Fracture and Branch Lopping
The decelerations caused by tree-trunk and branch fracture are given by
and
respectively. These expressions are found by again applying the conservation-of-energy Equation (5), with the energy consumption rate,
which is the total fracture energy per unit time for either the tree trunks or branches,
We have considered the case of branch fracture separately because often powder-snow avalanches will effectively lop the branches of trees, leaving the trunks standing. Note the appearance of the parameter dh, the mean branch spacing in the equation for
. Typical values for uf are given in Table 1.
Table 1. Bending fracture energies per cross-sectional area, uf
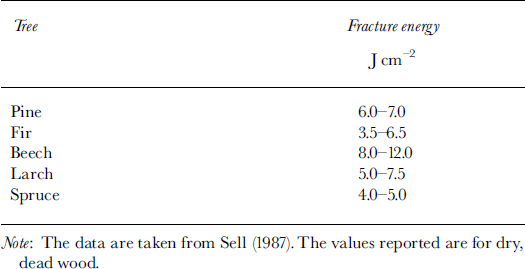
As an example, consider the deceleration of a 100 m long flowing avalanche (ρa =300kg m–3) with a flow height of 2 m when entering a larch stand (uf = 6 J cm–2, rt = 10 cm) with dw = 2 m and d1 = 1.0 m. The calculated deceleration is ait = –0.01 m s-2. This value should be placed in relation to the friction slope commonly assumed in avalanche-dynamics calculations for clear terrain. For example, the Swiss Guidelines assume for extreme avalanche events friction slopes near 0.16 g which is ten times larger than 0.01 m s–2
6. Tree Overturning
When trees overturn, a lump of soil is uprooted containing the root cluster and surrounding soil. Mattheck identified two primary lump shapes: a half-cylinder and a half-sphere (Reference Mattheck and BrelorMattheck and Brelor, 1993). In the following we will consider the case of a half-cylinder with failure radius rf and length 2rf. We assume that the failure surface of the lump lies outside the extent of the root cluster and that the overturning is governed by the strength of the soil and by rf. Trees with shallow root systems will have smaller rf values and subsequently smaller overturning energies. The fracture energy of the roots is not considered in the analysis.
The mass of the lump is
where ρo is the density of the soil. When the trees overturn they are pressed flat by the avalanche on to the ground surface. This means that the centroid of the half-cylinder is raised the vertical distance (see Fig. 3),
The energy required to raise the weight of the root-cluster
Although the cylinder rotates a total distance,
we will assume, however, for the energy analysis that the slip length, So, is given by
where δ is the angle of internal friction (see Fig. 6). The length of the slip surface is the length of the failure arc where the self-weight of the tree acts. After displacing this distance there is no resistance from the soil. The overturning energy of a single tree is thus
Fig. 6. Determination of the overturning energy of a single tree with cylindrical root lump with failure radius rf and length 2rf. We assume that the weight of the tree disperses with the angle of Internal friction, δ.
The force fo is the mean resisting force acting on the cylinder failure surface area parallel to the slip direction. The mean force is
where τf is the Mohr-Coulomb failure stress (Equation (2)),
The overburden stress, σz, acting on the slip surface is composed of two parts. The first, <rt, arises from the tree weight,
Since the weight of the tree disperses with the angle of internal friction of the soil, δ, the denominator in the above expression is
instead of
which it would be if the weight of the tree was acting over the entire slip surface. The internal friction angle 6 is expressed in radians. Thesecond part of the overburden stress, σo, arises from the weight of the lump. For this we take the stress at the lumpcenter of mass,
The mean shear stress on the slip surface is then
The total overturning work for a single tree, found from Equation (31), is
The factor
arises from the multiplication of the slip length So
with the mean force f0. Again, δ is expressed in radians. The total energy rate,
of tree overturning is a function of the number of trees the avalanche overturns per unit time,
When this value is substituted into the conservation-of-energy equation (Equation (5)), we find the deceleration of the avalanche caused by tree overturning is
The first term in the above equation arises from the Mohr-Coulomb failure criterion; the second term arises from raising the lump centroid. Note that the second term is a function of r4f. This implies that large amounts of energy can be consumed when raising the lump masses; however, this will probably not occur: the trees will fracture before trees with expansive root systems are overturned.
Considering an Alpine soil with 6 = 30°, c = 5kPa, ρo = 2000 kg m–3 and trees weighing mt = 1000 kg with rf = 2m, we find that the deceleration caused by raising the root cluster is greater than the work required to overcome the shear failure stress.
7. Runout Calculations
The Swiss Guidelines on avalanche-runout calculation employ the Voellmy-Salm model to predict runout distances (Reference VoellmyVoellmy, 1955; Reference Salm, Burkard and GublerSalm and others, 1990). Avalanche deceleration, avs, is governed by a dry-Coulomb-like friction and a velocity-dependent friction,
Suggested values for the parameters b and s are provided in the guidelines. These values have been determined by back-calculating observed avalanche events (Reference Buser and FrutigerBuser and Frutiger, 1980).
For flow in forests, the parameter s is approximately doubled; the dry-friction parameter remains unchanged.
The energy analysis allows us to determine how the friction parameters b and s should be modified to take into account flow through forests. Let Ab and As represent the increase in flow friction caused by tree entrainment and fracture. A comparison to Equation (20) (entrainment) and Equation (22) (trunk fracture) shows that
and
In order to double the velocity-dependent friction s (as specified by the Swiss Guidelines), requires a biomass loading (tree mass per square meter of forest) of the order
Table 2 presents some typical biomass loadings as a function of tree size, spacing and branch weights. Two conclusions can be drawn from Table 2. Firstly, the change in dry friction is small, thus confirming the guideline procedure of increasing only the velocity-dependent friction, and, secondly, the biomass loadings of typical forests are smaller than assumed by the Swiss Guidelines (Equation (43)). The mass entrained by the avalanche, however, will certainly be increased if the avalanche additionally erodes the snowpack and part of the soil cover. Field observations would support this supposition. Therefore, the entrained mass values required to double the velocity-dependent friction as specified by the Swiss Guidelines (Equation (43)) are easily attainable. For example, if an avalanche entrained a forest with mt/dwd1 = 150 kg m–2 (see Table 2), a 0.5 m high snowpack with a density of 300 kg m–3 and additionally 10 cm of soil with density ρ0 = 2000 kg m–3 then the total mass per square meter entrained by the avalanche is 500 kg m–2.
Table 2. Biomass loading and change in dry friction parameter b as a function of tree height ht, trunk radius τt, branch spacing dt, foliage height ht, branch weight mb and spacing dwd1
8. Example Calculations
A simple explicit time-integration procedure was written to track the motion of an avalanche given an initial size and velocity. The total acceleration of the avalanche is determined according to one of five cases:
-
(1) No forest
(44)
-
(2) Tree fracture and branch lopping
(45) -
(3) Tree fracture and entrainment
(46) -
(4) Overturning
(47) -
(5) Overturning and entrainment
(48)
Consider the following case: A flowing avalanche with dimensions h0 = 3m and l0 =100m is flowing with a velocity of 20 ms–1 down a 30° slope and impacts a 150 year old spruce forest. The average spacing of the trees is dw = d1 = 4 m. The trees have an average height of 20 m and girth of 40 cm (rt = 20 cm). The center of mass of the trees is located at Zt = 7.0 m. The tree branches are on average 3 m long with 5 cm radius. For 15 m of the tree’s length, five branches are located at 20 cm intervals. Since only half of the branches are fractured we find dh = 10 cm. The properties of the mountain soil are c = 5000 Pa, S = 30° and ρ0 = 2100 kg m–3. We assume that rf = lm.
Figures 7 and 8 compare the velocity of the avalanche over the flow distance for several cases. The results are always compared to the case of no forest to clearly show the influence of the forest. Note that the avalanche is moving down a steep slope and thus continues to accelerate over the distance of 750 m.
Fig. 7. Tree fracture, (a) Comparison of the velocity of the avalanche over open terrain and over forested terrain when 150 year old spruce trees fail by trunk fracture (no difference betwen the two curves), (b) The fractured trees are entrained in the flow, decreasing the flow velocity.
Fig. 8. Tree overturning. (a) Comparison of the velocity of the avalanche over open terrain and over forested terrain when 150 year old spruce trees are overturned, (b) The overturned trees are entrained in the flow. Avalanches can be decelerated if they entrain the heavy root cluster.
The calculations clearly show that the avalanches are not decelerated by fracturing or overturning trees, but rather by entraining them into the flow. There is no significant difference between the no-forest case and the cases of tree fracture and tree overturning. Although entraining fractured tree debris slows the avalanche down, the deceleration may not be significant. Instead of reaching a velocity of 45 m s–1, the avalanche reaches a velocity of 42 ms–1. The reason why tree overturning with entrainment decelerates the avalanche more noticeably (the avalanche reaches a velocity of only 27 ms–1) is that the heavy root cluster is entrained in the flow.
The avalanche had a relatively small initial volume of 30 000 m3. Larger avalanches would be slowed down even less.
In the second example, we consider the case of an avalanche of the same size and velocity (ho = 3 m, l0 = 100 m, u0= 20 ms–1) impacting a 30 year old forest containing trees of smaller height (ht = 5 m) and girth (rt = 7 cm). The trees are spaced dl = dw = 1.5m apart. The slope angle, the properties of the soil (δ and c) and wood remain unchanged. We compare two cases: tree fracture with entrainment and tree overturning without entrainment. We assume that the failure radius of the root system is rf = 100 cm. The results are displayed in Figure 9. In this example, tree overturning decelerates the avalanche more than trunk fracture with entrainment.
Fig. 9. The difference between tree fracture with entrainment and tree overturning. An avalanche of 30 000 m3 impacts a 30year old forest. The overturning failure radius of the ht = 5 m trees is rf =100 cm. (a) Avalanche deceleration when the trees fracture and are entrained inflow, (b) Avalanche deceleration when the trees overturn.
9. Conclusions
In this paper we presented a simple center-of-mass avalanche model that accounts for avalanche flow in forests and distinguishes between two different modes of tree failure: fracture and overturning (with or without debris entrainment). We showed that large avalanches can destroy forests without significant deceleration. This fact explains the observations of the 1951 and 1999 winters where avalanches flowed long distances while destroying large tracts of forests.
The analysis procedure relates forest properties directly to avalanche-flow friction parameters. The energy analysis avoids the problem of determining how the destructive force of avalanches is applied to fracture or overturn trees. However, it cannot predict for what avalanche size or flow velocity the trees will be destroyed, since this requires knowing how the force is applied to the trees. The energy analysis assumes that the avalanches are sufficiently large to destroy the forests.
We expressed avalanche deceleration in terms of Swiss Guideline friction parameters. We showed that the velocity-dependent friction accounts for tree, snow and soil-cover entrainment. The dry-Coulomb friction parameter can be modified to include tree fracture and overturning.
Our calculations revealed that debris entrainment slows down an avalanche more than tree fracture. If a storm damages a protective forest it would therefore be advantageous to keep the tree debris in place. We also showed that an older forest can decelerate smaller avalanches (say, <30 000 m3) significantly when the trees overturn and the avalanche entrains the heavy root cluster. In all cases, when the trees fracture they consume very little of the avalanche’s flow energy.
In conclusion, we believe that the most important contribution of this paper is that it relates parameters such as tree spacing, girth and height to the deceleration of avalanches. In future, this will help practitioners to classify forest damage (fracture and overturning), understand avalanche events better (why an avalanche stopped or flowed a long distance), provide a scientific method to investigate the mechanical properties of forests and trees, and finally to care for mountain forests so that they always, irrespective of age, provide the maximum protective capacity against snow avalanches.
