Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T10:08:55.385Z Has data issue: false hasContentIssue false
  • English
  • Français

On the support of extremal martingale measures with given marginals: the countable case

Part of: Stochastic processes Mathematical finance

Published online by Cambridge University Press:  07 August 2019

Luciano Campi  and
Claude Martini
Luciano Campi*
Affiliation:
London School of Economics and Political Science
Claude Martini*
Affiliation:
Zeliade Systems
*
*Postal address: London School of Economics and Political Science, Houghton Street, London, WC2A 2AE, UK.
**Postal address: Zeliade Systems, 56 Rue Jean-Jacques Rousseau, 75001 Paris, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the supports of extremal martingale measures with prespecified marginals in a two-period setting. First, we establish in full generality the equivalence between the extremality of a given measure Q and the denseness in 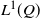$L^1(Q)$ of a suitable linear subspace, which can be seen in a financial context as the set of all semistatic trading strategies. Moreover, when the supports of both marginals are countable, we focus on the slightly stronger notion of weak exact predictable representation property (WEP) and provide two combinatorial sufficient conditions, called the ‘2-link property’ and ‘full erasability’, on how the points in the supports are linked to each other for granting extremality. When the support of the first marginal is a finite set, we give a necessary and sufficient condition for the WEP to hold in terms of the new concepts of 2-net and deadlock. Finally, we study the relation between cycles and extremality.

Keywords

Model-free pricingextremal measuremartingale optimal transportweak predictable representation propertycycle

MSC classification

Primary: 60G42: Martingales with discrete parameter
Secondary: 91G80: Financial applications of other theories (stochastic control, calculus of variations, PDE, SPDE, dynamical systems)
Type
Original Article
Information
Advances in Applied Probability , Volume 51 , Issue 2 , June 2019 , pp. 570 - 605
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acciaio, B., Larsson, M. and Schachermayer, W. (2017). The space of outcomes of semi-static trading strategies need not be closed. Finance Stoch. 21, 741–751.CrossRefGoogle Scholar
Aliprantis, C. D., and Border, K. C. (1994). Infinite-Dimensional Analysis. Springer, Berlin.CrossRefGoogle Scholar
Beiglböck, M., Henry-Labordère, P. and Penkner, F. (2013). Model-independent bounds for option prices: a mass transport approach. Finance Stoch. 17, 477–501.CrossRefGoogle Scholar
Beiglböck, M. and Juillet, N. (2016). On a problem of optimal transport under marginal martingale constraints. Ann. Prob. 44, 42–106.CrossRefGoogle Scholar
Beneš, V. and Štĕpán, J. (1987). The support of extremal probability measures with given marginals. Math. Statist. Prob. Theory A, 33–41.CrossRefGoogle Scholar
Bianchini, S. and Caravenna, L. (2009). On the extremality, uniqueness and optimality of transference plans. Bull. Inst. Math. Acad. Sin. (N.S.) 4, 353–454.Google Scholar
Birkhoff, G. (1946). Three observations on linear algebra. Univ. Nac. Tucumán. Revista A 5, 147–151.Google Scholar
Breeden, D. T., and Litzenberger, R. H. (1978). Prices of state-contingent claims implicit in option prices. J. Business 51, 621–651.CrossRefGoogle Scholar
Campi, L. (2004). A note on extremality and completeness in financial markets with infinitely many risky assets. Rend. Sem. Mat. Univ. Padova 112, 181–198.Google Scholar
Campi, L. (2004). Arbitrage and completeness in financial markets with given N-dimensional distributions. Decisions Economics Finance 27, 57–80.CrossRefGoogle Scholar
Dellacherie, C. (1968). Une représentation intégrale des surmartingales à temps discret. Publ. Inst. Statist. Univ. Paris 17, 1–17.Google Scholar
Denny, J. L. (1980). The support of discrete extremal measures with given marginals. Michigan Math. J. 27, 59–64.Google Scholar
Diestel, R. (2005). Graph Theory (Grad. Texts Math. 173). Springer, Berlin.Google Scholar
Douglas, R. G. (1964). On extremal measures and subspace density. Michigan Math. J. 11, 243–246.Google Scholar
Galichon, A., Henry-Labordere, P. and Touzi, N. (2014). A stochastic control approach to no-arbitrage bounds given marginals, with an application to lookback options. Ann. Appl. Prob. 24, 312–336.CrossRefGoogle Scholar
Henry-Labordere, P. and Touzi, N. (2016). An explicit martingale version of the one-dimensional Brenier theorem. Finance Stoch. 20, 635–668.CrossRefGoogle Scholar
Hestir, K. and Williams, S. C. (1995). Supports of doubly stochastic measures. Bernoulli 1, 217–243.CrossRefGoogle Scholar
Hobson, D. G. (1998). Robust hedging of the lookback option. Finance Stoch. 2, 329–347.CrossRefGoogle Scholar
Hobson, D. and Klimmek, M. (2015). Robust price bounds for the forward starting straddle. Finance Stoch. 19, 189–214.CrossRefGoogle Scholar
Hobson, D. and Neuberger, A. (2012). Robust bounds for forward start options. Math. Finance 22, 31–56.CrossRefGoogle Scholar
Kellerer, H. G. (1964). Verteilungsfunktionen mit gegebenen Marginalverteilungen. Z. Wahrscheinlichkeitsth. 3, 247–270.CrossRefGoogle Scholar
Kłopotowski, A., Nadkarni, M. G. and Bhaskara Rao, K. P. S. (2003). When is $f (x_1, x_2,\ldots , x_n) = u_1 (x_1)+ u_2 (x_2)+ \cdots + u_n (x_n) $ ? In Proceedings of the Indian Academy of Sciences: Mathematical Sciences, Vol. 113, pp. 77–86.Google Scholar
Kłopotowski, A., Nadkarni, M. G., and Bhaskara Rao, K. P. S. (2004). Geometry of good sets in n-fold Cartesian product. In Proceedings of the Indian Academy of Sciences: Mathematical Sciences, Vol. 114, pp. 181–197.CrossRefGoogle Scholar
Jacod, J. and Shiryaev, A. N. (1998). Local martingales and the fundamental asset pricing theorems in the discrete-time case. Finance Stoch. 2, 259–273.CrossRefGoogle Scholar
Letac, G. (1966). Representation des mesures de probabilité sur le produit de deux espaces denombrables, de marges données. Illinois J. Math. 10, 497–507.CrossRefGoogle Scholar
Lick, D. R. and White, A. T. (1970). k-degenerate graphs. Canad. J. Math. 22, 1082–1096.CrossRefGoogle Scholar
Lindenstrauss, J. (1965). A remark on extreme doubly stochastic measures. Amer. Math. Monthly 72, 379–382.Google Scholar
Mukerjee, H. G. (1985). Supports of extremal measures with given marginals. Illinois J. Math. 29, 248–260.CrossRefGoogle Scholar
Naumark, M. A. (1946). On extremal spectral functions of a symmetric operator. C. R. (Doklady) Acad. Sci. URSS (N.S.) 54, 7–9.Google Scholar
Pallottini, R. (2018). Misure estremali per il trasporto di massa con vincoli di martingala. Thesis, Università degli Studi dell’Aquila.Google Scholar
Revuz, D., and Yor, M. (2013). Continuous Martingales and Brownian Motion (Fundamental Principles Math. Sci. 293). Springer Science & Business Media.Google Scholar
Strassen, V. (1965). The existence of probability measures with given marginals. Ann. Math. Statist. 36, 423–439.CrossRefGoogle Scholar
Villani, C. (2008). Optimal Transport: Old and New (Fundamental Principles Math. Sci. 338). Springer Science & Business Media.Google Scholar