Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T04:58:52.563Z Has data issue: false hasContentIssue false
  • English
  • Français

Multivariate hazard rates and stochastic ordering

Published online by Cambridge University Press:  01 July 2016

Moshe Shaked  and
J. George Shanthikumar
Moshe Shaked*
Affiliation:
University of Arizona
J. George Shanthikumar*
Affiliation:
University of California, Berkeley
*
∗Postal address: Department of Mathematics, The University of Arizona, Tucson, AZ 85721, USA.
∗∗ Postal address: School of Business Administration, University of California, Berkeley, CA 94720, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

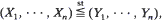Properties of the conditional hazard rates of X1, · ··, Xn and Y1, · ··, Yn, which imply (X1, · ··, Xn) (Y1, · ··, Yn), are found. These are used to find conditions on the hazard rates of T = (T1, · ··, Tn) which ensure that T has the MIHR | property of Arjas (1981a) and the ‘weakened by failure’ property of Arjas and Norros (1984). Applications for load-sharing model and multivariate imperfect repair are given.

Keywords

ASSOCIATED RANDOM VARIABLESIMPERFECT REPAIRIHRIHRANBU
Type
Research Article
Information
Advances in Applied Probability , Volume 19 , Issue 1 , March 1987 , pp. 123 - 137
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by the Air Force Office of Scientific Research, USAF, under Grant AFOSR-84-0205. Reproduction in whole or in part is permitted for any purpose of the United States government.

References

Arjas, E. (1981a) A stochastic process approach to multivariate reliability: notions based on conditional stochastic order. Math. Operat. Res. 6, 263–276.Google Scholar
Arjas, E. (1981b) The failure and hazard processes in multivariate reliability systems. Math. Operat. Res. 6, 551–562.CrossRefGoogle Scholar
Arjas, E. and Norros, I. (1984) Life lengths and association: a dynamic approach. Math. Operat. Res. 9, 151–158.CrossRefGoogle Scholar
Block, H. W., Borges, W. S. and Savits, T. H. (1985) Age dependent minimal repair. J. Appl. Prob. 22, 370–385.CrossRefGoogle Scholar
Bremaud, P. (1981) Point Processes and Queues. Springer-Verlag, New York.CrossRefGoogle Scholar
Brown, M. and Proschan, F. (1983) Imperfect repair. J. Appl. Prob. 20, 851–859.CrossRefGoogle Scholar
Cox, D. R. (1972) Regression models and life tables (with discussion). J. R. Statist. Soc. B 34, 187–220.Google Scholar
Cox, D. R. and Lewis, P. A. W. (1972) Multivariate point processes. Proc. 6th Berkeley Symp. Math. Statist. Prob. 3, 401–488.Google Scholar
Esary, J. D. and Marshall, A. W. (1970) Coherent life functions. SIAM J. Appl. Math. 18, 810–814.CrossRefGoogle Scholar
Esary, J. D., Proschan, F. and Walkup, D. W. (1967) Association of random variables, with applications. Ann. Math. Statist. 38, 1466–1474.CrossRefGoogle Scholar
Freund, J. E. (1961) A bivariate extension of the exponential distribution. J. Amer. Statist. Assoc. 56, 971–977.CrossRefGoogle Scholar
Kopocinska, I. and Kopocinski, B. (1980) On system reliability under random load of elements. Zastos Mat. XVII, 5–13.Google Scholar
Marshall, A. W. and Shaked, M. (1986) Multivariate new better than used distributions. Math. Oper. Res. 11, 110–116.CrossRefGoogle Scholar
Norros, I. (1985) Systems weakened by failure. Stoch. Proc. Appl. 20, 181–196.Google Scholar
Norros, I. (1984) A compensator representation of multivariate lifelengths distributions, with applications. Scand. J. Statist. To appear.Google Scholar
Ross, S. M. (1984) a model in which component failure rates depend on the working set. Naval Res. Log. Quart. 31, 297–301.CrossRefGoogle Scholar
Schechner, Z. (1984) A load-sharing model: the linear breakdown rule. Naval Res. Log. Quart. 31, 137–144.Google Scholar
Shaked, M. and Shanthikumar, J. G. (1984) Multivariate hazard rates and stochastic ordering. Technical report, Department of Mathematics, University of Arizona.Google Scholar
Shaked, M. and Shanthikumar, J. G. (1986) Multivariate imperfect repair. Operat. Res. To appear.CrossRefGoogle Scholar