We show that the Virasoro conjecture in Gromov–Witten theory holds for the the total space of a toric bundle 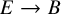 $E \to B$ if and only if it holds for the base B. The main steps are: (i) We establish a localization formula that expresses Gromov–Witten invariants of E, equivariant with respect to the fiberwise torus action in terms of genus-zero invariants of the toric fiber and all-genus invariants of B, and (ii) we pass to the nonequivariant limit in this formula, using Brown’s mirror theorem for toric bundles.
$E \to B$ if and only if it holds for the base B. The main steps are: (i) We establish a localization formula that expresses Gromov–Witten invariants of E, equivariant with respect to the fiberwise torus action in terms of genus-zero invariants of the toric fiber and all-genus invariants of B, and (ii) we pass to the nonequivariant limit in this formula, using Brown’s mirror theorem for toric bundles.