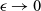1 results
Homogenisation of a two-phase problem with nonlinear dynamic Wentzell-interface condition for connected–disconnected porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 617-641
-
- Article
-
- You have access
- HTML
- Export citation
-
We investigate a reaction–diffusion problem in a two-component porous medium with a nonlinear interface condition between the different components. One component is connected and the other one is disconnected. The ratio between the microscopic pore scale and the size of the whole domain is described by the small parameter
$\epsilon$. On the interface between the components, we consider a dynamic Wentzell-boundary condition, where the normal fluxes from the bulk domains are given by a reaction–diffusion equation for the traces of the bulk solutions, including nonlinear reaction kinetics depending on the solutions on both sides of the interface. Using two-scale techniques, we pass to the limit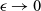 
$\epsilon \to 0$ and derive macroscopic models, where we need homogenisation results for surface diffusion. To cope with the nonlinear terms, we derive strong two-scale convergence results.
