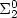In this paper, we address the problem of defining a fixpoint semantics for Constraint Handling Rules (CHR) that captures the behavior of both simplification and propagation rules in a sound and complete way with respect to their declarative semantics. Firstly, we show that the logical reading of states with respect to a set of simplification rules can be characterized by a least fixpoint over the transition system generated by the abstract operational semantics of CHR. Similarly, we demonstrate that the logical reading of states with respect to a set of propagation rules can be characterized by the greatest fixpoint. Then, in order to take advantage of both types of rules without losing fixpoint characterization, we present a new operational semantics with persistent constraints.

We finally establish that this semantics can be characterized by two nested fixpoints, and we show that the resulting language is an elegant framework to program using coinductive reasoning.

Drawing on an analogy with temporal fixpoint logic, we relate the arithmetic fixpoint definable sets to the winning positions of certain games, namely games whose winning conditions lie in the difference hierarchy over $\Sigma^0_2$. This both provides a simple characterization of the fixpoint hierarchy, and refines existing results on the power of the game quantifier in descriptive set theory. We raise the problem of transfinite fixpoint hierarchies.