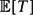NP-complete problems should be hard on some instances but those may be extremely rare. On generic instances many such problems, especially related to random graphs, have been proved to be easy. We show the intractability of random instances of a graph colouring problem: this graph problem is hard on average unless all NP problems under all samplable (i.e. generatable in polynomial time) distributions are easy. Worst case reductions use special gadgets and typically map instances into a negligible fraction of possible outputs. Ours must output nearly random graphs and avoid any super-polynomial distortion of probabilities. This poses significant technical difficulties.

Suppose that X1, X2, . . . are independent identically distributed Bernoulli random variables with mean p. A Bernoulli factory for a function f takes as input X1, X2, . . . and outputs a random variable that is Bernoulli with mean f(p). A fast algorithm is a function that only depends on the values of X1, . . ., XT, where T is a stopping time with small mean. When f(p) is a real analytic function the problem reduces to being able to draw from linear functions Cp for a constant C > 1. Also it is necessary that Cp ⩽ 1 − ε for known ε > 0. Previous methods for this problem required extensive modification of the algorithm for every value of C and ε. These methods did not have explicit bounds on 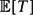$\mathbb{E}[T]$ as a function of C and ε. This paper presents the first Bernoulli factory for f(p) = Cp with bounds on 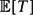$\mathbb{E}[T]$ as a function of the input parameters. In fact, supp∈[0,(1−ε)/C]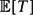$\mathbb{E}[T]$ ≤ 9.5ε−1C. In addition, this method is very simple to implement. Furthermore, a lower bound on the average running time of any Cp Bernoulli factory is shown. For ε ⩽ 1/2, supp∈[0,(1−ε)/C]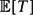$\mathbb{E}[T]$≥0.004Cε−1, so the new method is optimal up to a constant in the running time.