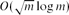1 results
Applications of a New Separator Theorem for String Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 25 October 2013, pp. 66-74
-
- Article
- Export citation
-
An intersection graph of curves in the plane is called a string graph. Matoušek almost completely settled a conjecture of the authors by showing that every string graph with m edges admits a vertex separator of size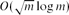
$O(\sqrt{m}\log m)$. In the present note, this bound is combined with a result of the authors, according to which every dense string graph contains a large complete balanced bipartite graph. Three applications are given concerning string graphs G with n vertices: (i) if Kt ⊈ G for some t, then the chromatic number of G is at most (log n)O(log t); (ii) if Kt,t ⊈ G, then G has at most t(log t)O(1)n edges,; and (iii) a lopsided Ramsey-type result, which shows that the Erdős–Hajnal conjecture almost holds for string graphs.
