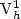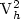This paper is devoted to Eulerian models for incompressible fluid-structure systems. These models are primarily derived for computational purposes as they allow to simulate in a rather straightforward way complex 3D systems. We first analyze the level set model of immersed membranes proposed in [Cottet and Maitre, Math. Models Methods Appl. Sci.16 (2006) 415–438]. We in particular show that this model can be interpreted as a generalization of so-called Korteweg fluids. We then extend this model to more generic fluid-structure systems. In this framework, assuming anisotropy, the membrane model appears as a formal limit system when the elastic body width vanishes. We finally provide some numerical experiments which illustrate this claim.

The aim of the topological asymptotic analysis is to provide an asymptotic expansion of a shape functional with respect to the size of a small inclusion inserted inside the domain. The main field of application is shape optimization. This paper addresses the case of the steady-state Navier-Stokes equations for an incompressible fluid and a no-slip condition prescribed on the boundary of an arbitrary shaped obstacle. The two and three dimensional cases are treated for several examples of cost functional and a numerical application is presented.

In this paper, a general technique is developed to enlarge the velocity space ${\rm V}_h^1$ 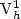of the unstable -element by adding spaces ${\rm V}_h^2$ 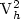such thatfor the extended pair the Babuska-Brezzi condition is satisfied. Examplesof stable elements which can be derived in such a way imply the stability of the well-knownQ2/Q1 -element and the 4Q1/Q1 -element. However, our new elementsare much more cheaper. In particular, we shall see that more than half of theadditional degrees of freedom when switching from the Q 1 to the Q 2 and4Q1 , respectively, element are not necessary to stabilize theQ1/Q1 -element. Moreover, by using the technique of reduced discretizationsand eliminating the additional degrees of freedom we showthe relationship between enlarging the velocity space and stabilized methods. This relationship has been established for triangular elements but was not known for quadrilateral elements. As a result we derive new stabilizedmethods for the Stokes and Navier-Stokes equations. Finally, we showhow the Brezzi-Pitkäranta stabilization and the SUPG method for theincompressible Navier-Stokes equations can be recovered as special cases of the general approach. In contrast to earlier papers we do not restrict ourselves to linearized versions of the Navier-Stokes equations but deal with the full nonlinear case.

We study the local exact controllability problem for the Navier-Stokes equations that describe an incompressible fluid flow in abounded domain with control distributed in an arbitrary fixed subdomain. The result that we obtain in this paper is as follows.Suppose that we have a given stationary point of the Navier-Stokes equations and our initial condition is sufficiently close to it. Thenthere exists a locally distributed control such that in a given moment of time the solution of the Navier-Stokes equations coincideswith this stationary point.