1 results
Well-timed diffusion approximations
-
- Journal:
- Advances in Applied Probability / Volume 13 / Issue 2 / June 1981
- Published online by Cambridge University Press:
- 01 July 2016, pp. 352-368
- Print publication:
- June 1981
-
- Article
- Export citation
-
Let X be a Markov process on the line. Under certain conditions it is possible to find a diffusion process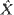
which is an approximation to X in the following sense:(1) X can be embedded in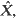
that is there are stopping times (Tt) such that {Xt, t ≥ 0} and 
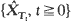have the same distribution;(2) for each t, E{Tt} = t.
We call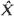
the well-timed diffusion approximation to X, and suggest that it is useful for approximating quantities like the first-exit probabilities and expected first-exit times of X.We determine the well-timed approximation in several special cases and give an asymptotic approximation for use in cases in which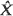
cannot be exactly determined.
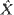which is an approximation to 
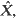that is there are stopping times (
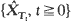have the same distribution;
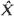the well-timed diffusion approximation to 
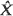cannot be exactly determined.