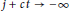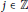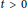This work investigates the existence and bifurcation structure of multi-pulse steady-state solutions to bistable lattice dynamical systems. Such solutions are characterized by multiple compact disconnected regions where the solution resembles one of the bistable states and resembles another trivial bistable state outside of these compact sets. It is shown that the bifurcation curves of these multi-pulse solutions lie along closed and bounded curves (isolas), even when single-pulse solutions lie along unbounded curves. These results are applied to a discrete Nagumo differential equation and we show that the hypotheses of this work can be confirmed analytically near the anti-continuum limit. Results are demonstrated with a number of numerical investigations.

In this paper, we study a two-component Lotka–Volterra competition systemon a one-dimensional spatial lattice. By the comparison principle, together with the weighted energy, we prove that the traveling wavefronts with large speed are exponentially asymptotically stable, when the initial perturbation around the traveling wavefronts decays exponentially as 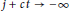$j\,+\,ct\,\to \,-\,\infty $, where 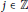$j\,\in \,\mathbb{Z}$, 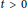$t\,>\,0$, but the initial perturbation can be arbitrarily large on other locations. This partially answers an open problem by J.-S. Guo and C.-H.Wu.