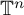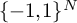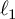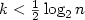We prove stronger variants of a multiplier theorem of Kislyakov. The key ingredients are based on ideas of Kislyakov and the Kahane–Salem–Zygmund inequality. As a by-product, we show various multiplier theorems for spaces of trigonometric polynomials on the n-dimensional torus $\mathbb {T}^n$ or Boolean cubes $\{-1,1\}^N$. Our more abstract approach based on local Banach space theory has the advantage that it allows to consider more general compact abelian groups instead of only the multidimensional torus. As an application, we show that various recent $\ell _1$-multiplier theorems for trigonometric polynomials in several variables or ordinary Dirichlet series may be proved without the Kahane–Salem–Zygmund inequality.

We investigate the structure of “worst-case” quasi reduced ordered decision diagrams and Boolean functions whose truth tables are associated to: we suggest different ways to count and enumerate them. We, then, introduce a notion of complexity which leads to the concept of “hard” Boolean functions as functions whose QROBDD are “worst-case” ones. So we exhibit the relation between hard functions and the Storage Access function (also known as Multiplexer).

We study deterministic one-way communication complexity of functions with Hankel communication matrices. Some structural properties of such matrices are established and applied to the one-way two-party communication complexity of symmetric Boolean functions. It is shown that the number of required communication bits does not depend on the communication direction, provided that neither direction needs maximum complexity. Moreover, in order to obtain an optimal protocol, it is in any case sufficient to consider only the communication direction from the party with the shorter input to the other party. These facts do not hold for arbitrary Boolean functions in general. Next, gaps between one-way and two-way communication complexity for symmetric Boolean functions are discussed. Finally, we give some generalizations to the case of multiple parties.

In this paper we investigate the theoretical foundation of a new bottom-up semantics for linear logic programs, and more precisely for the fragment of LinLog (Andreoli, 1992) that consists of the language LO (Andreoli & Pareschi, 1991) enriched with the constant 1. We use constraints to symbolically and finitely represent possibly infinite collections of provable goals. We define a fixpoint semantics based on a new operator in the style of TP working over constraints. An application of the fixpoint operator can be computed algorithmically. As sufficient conditions for termination, we show that the fixpoint computation is guaranteed to converge for propositional LO. To our knowledge, this is the first attempt to define an effective fixpoint semantics for linear logic programs. As an application of our framework, we also present a formal investigation of the relations between LO and Disjunctive Logic Programming (Minker et al., 1991). Using an approach based on abstract interpretation, we show that DLP fixpoint semantics can be viewed as an abstraction of our semantics for LO. We prove that the resulting abstraction is correct and complete (Cousot & Cousot, 1977; Giacobazzi & Ranzato, 1997) for an interesting class of LO programs encoding Petri Nets.

We construct, for each integer n, three functions from {0,1}n to {0,1} such that any boolean mapping from {0,1}n to {0,1}n can be computed with a finite sequence of assignations only using the n input variables and those three functions.

Communication complexity of two-party (multiparty)protocols has established itself as a successful method for proving lower bounds on the complexity of concrete problems for numerous computing models. While the relations between communication complexity and oblivious, semilective computations are usually transparent and the main difficulty is reduced to proving nontrivial lower bounds on the communication complexity of given computing problems, the situation essentially changes, if one considers non-oblivious or multilective computations. The known lower bound proofs for such computations are far from being transparent and the crucial ideas of these proofs are often hidden behind some nontrivial combinatorial analysis. The aim of this paper is to create a general framework for the use of two-party communication protocols for lower bound proofs on multilective computations. The result of this creation is not only a transparent presentation of some known lower bounds on the complexity of multilective computations on distinct computing models, but also the derivation of new nontrivial lower bounds on multilective VLSI circuits and multilective planar Boolean circuits.In the case of VLSI circuits we obtain a generalization ofThompson's lower bounds on AT 2 complexity for multilective circuits.The Ω(n 2) lower bound on the number of gates of any k-multilectiveplanar Boolean circuit computing a specific Boolean function of n variablesis established for $k<\frac{1}{2} \log_2 n$ . Another advantage of this framework is that it provides lower bounds for a lot of concrete functions. This contrasts to the typical papersdevoted to lower bound proofs, where one establishes a lower bound for one or a few specific functions.